Две основные задачи динамики точки
Первая (прямая) задача динамики точки. Известно движение точки, необходимо найти приложенную к точке силу. Математически эта задача решается дифференцированием заданных кинематических уравнений движения (ч. 2, п. 2.2.1).
Вторая (обратная) задача динамики точки. Известны приложенные к точке силы. Необходимо узнать, как точка движется, то есть найти кинематические уравнения движения точки. Математически эта задача решается интегрированием дифференциальных уравнений движения (п. 3.2.1). Возникающие при этом постоянные интегрирования находятся из начальных условий.
В общем случае обратная задача динамики точки является более сложной из-за математических трудностей при интегрировании дифференциальных уравнений. Приложенная к точке сила F может быть постоянной по величине (например, сила тяжести вблизи поверхности Земли); может быть функцией только времени t (например, внешнее силовое воздействие при колебаниях точки); может быть функцией только скорости точки v (например, сила сопротивления); может быть функцией только положения точки s (например, сила упругости); и, наконец, может зависеть от нескольких из этих аргументов одновременно. Способы интегрирования дифференциальных уравнений движения при этом разные (табл. 3.1). Аналитически в конечном виде обратная задача динамики может быть решена лишь для сравнительно небольшого числа простейших случаев, если функции 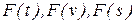 , а в общем случае
, а в общем случае 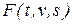 являются интегрируемыми.
являются интегрируемыми.
Таблица 3.1. Интегрирование дифференциальных уравнений движения точки в простейших случаях
| Дифференциальное уравнение движения, сила зависит | Скорость точки | Кинематическое уравнение (закон) движения |
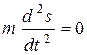 , сила не действует , сила не действует
| 
| 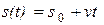
|
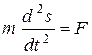 , сила постоянна , сила постоянна
| 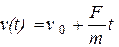
| 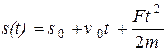
|
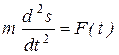 , от времени , от времени
| 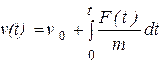
| 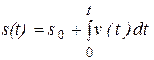
|
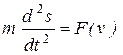 , от скорости , от скорости
| Находится из уравнения
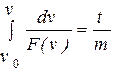
| 
|
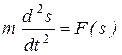 , от положения , от положения
| 
| Находится из уравнения
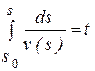
|
Примечание: Во всех случаях приняты начальные условия 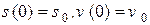 .
Обозначения: s – координата, .
Обозначения: s – координата, 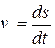 - скорость точки. - скорость точки.
|
Дата добавления: 2014-12-01; просмотров: 1055;
