Задача Галилея
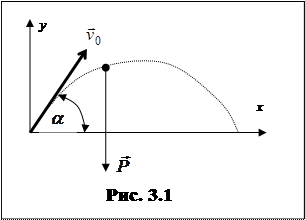 Рассмотрим движение материальной точки, брошенной с начальной скоростью
Рассмотрим движение материальной точки, брошенной с начальной скоростью  под углом
под углом 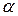 к горизонту, в среде без сопротивления (рис. 3.1).
к горизонту, в среде без сопротивления (рис. 3.1).
Точка является свободной, к ней во все время движения приложена только сила тяжести 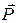 , модуль которой выражается через массу точки
, модуль которой выражается через массу точки 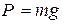 . Дифференциальные уравнения движения точки в координатной форме имеют вид:
. Дифференциальные уравнения движения точки в координатной форме имеют вид: 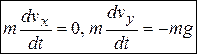 . Последовательно интегрируем дифференциальные уравнения. Из первого уравнения
. Последовательно интегрируем дифференциальные уравнения. Из первого уравнения 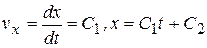 , из второго уравнения
, из второго уравнения 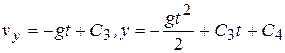 . Постоянные интегрирования С находим из начальных условий
. Постоянные интегрирования С находим из начальных условий 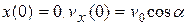 ,
, 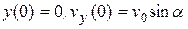 :
: 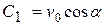 ,
,  ,
, 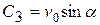 ,
, 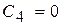 . Окончательно кинематические уравнения движения точки имеют вид:
. Окончательно кинематические уравнения движения точки имеют вид: 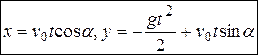 .
.
Дата добавления: 2014-12-01; просмотров: 2679;
