Свободные колебания материальной точки

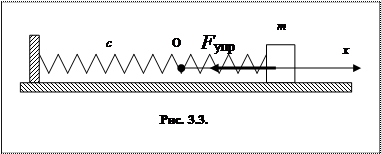Если материальная точка массой m прикреплена к концу пружины жесткостью с, со стороны пружины на точку действует восстанавливающая сила – сила упругости 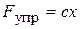, зависящая от положения точки – координаты x, отсчитываемой от точки О - правого конца недеформированной пружины (рис. 3.3). Дифференциальное уравнение в проекции на ось Оx имеет вид: .

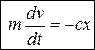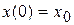Такое уравнение можно решить разделением переменных, если воспользоваться подстановкой . С учетом начальных условий (начальное смещение точки от положения О статического равновесия) и 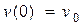(начальная скорость точки) зависимость скорости v от координаты x находится интегрированием . Затем кинематическое уравнение движения находится по алгоритму, определенному в табл. 3.1 (случай зависимости силы от положения точки). Окончательно оно имеет вид уравнения свободных гармонических колебаний: 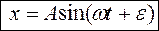, где 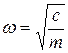- собственная частота колебаний, 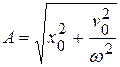- амплитуда свободных колебаний, - начальная фаза колебаний.