Теоремы о моментах инерции
Для определения моментов инерции тел относительно других осей используют теорему Штейнера-Гюйгенса: момент инерции тела относительно оси z равен сумме момента инерции этого тела относительно оси zc , параллельной оси z и проходящей через центр масс С тела (табл. 3.2), и произведения массы m тела на квадрат расстояния d между осями z и zc: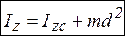 
.
Момент инерции тела относительно любой оси u, проходящей через какую-либо точку О, связаны с моментами инерции этого тела относительно осей x, y, z, начало которой совпадает с точкой О, следующим соотношением: 
где 
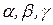- углы, образуемые осью u с осями x, y, z.
Центробежные моменты инерции 
тела относительно соответствующих осей определяются по аналогии с осевым моментом инерции (п. 3.3.2), например: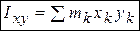 
.
Дата добавления: 2014-12-01; просмотров: 1370;