Момент инерции. Теорема Штейнера

Момент инерции

Моментом инерции тела (механической системы) относительно оси вращения есть физическая величина, равная сумме произведений масс n материальных точек на квадраты их расстояний до рассматриваемой оси:

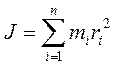
В случае непрерывного распределения масс эта сумма сводится к интегралу, где интегрирование производится по всему объему тела. Величина r в данном случае есть функция положения точки с координатами x, y, z:

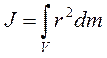
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис.7.1):

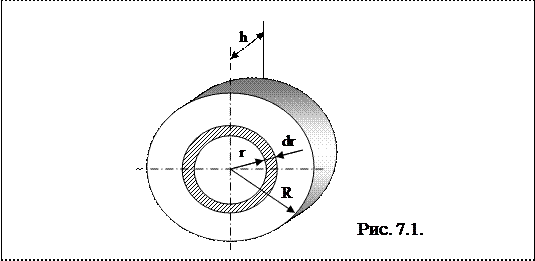
Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r + dr.

Теорема Штейнера

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера:

Момент инерции тела J относительно любой оси вращения равен моменту его инерции J_c относительно параллельной оси, проходящей через центр масс тела С, сложенному с произведением массы тела m на квадрат расстояния а между осями:

Моменты инерции однородных тел , имеющих массу m, равномерно распределенную по объему, и правильную геометрическую форму:

Тело	Положение оси вращения	Момент инерции
Труба (полый тонкостенный цилиндр) радиуса R	Ось симметрии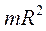
Цилиндр сплошной или диск радиуса R	Ось симметрии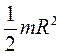
Стержень прямой тонкий, длиной l	Ось перпендикулярна стержню и проходит через его середину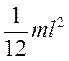
Шар радиусом R	Ось проходит через центр шара

Пример: Найти момент инерции стержня длиной l относительно оси, которая перпендикулярна стержню и проходит через его конец (т.е. ).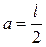

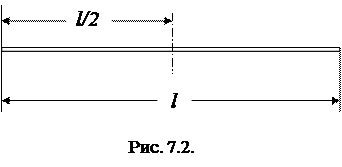
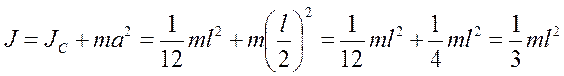
Таким образом, величина момента инерции зависит от выбора оси вращения. Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.

Момент силы

Момент силы относительно неподвижной точки О

- называется физическая величина, определяемая векторным произведением радиуса-вектора 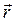, проведенного из точки О в точку А приложения силы, на силу 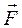(см. рисунок 7.3.):

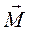Здесь - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 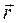к .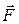

Модуль момента силы:

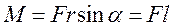, где

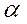- угол между 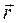и ;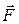

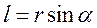- плечо силы - кратчайшее расстояние между линией действия силы и точкой О.

Момент силы относительно неподвижной оси Z

Моментом силы относительно неподвижной оси Z называется скалярная величина 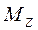, равная проекции на эту ось вектора 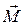момента силы, определенного относительно произвольной точки О данной оси Z (Рис.7.4).

Рис. 7.4.

Значение момента 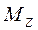не зависит от выбора положения точки О на оси Z.