Абсолютно неупругий удар
Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое тело.
Согласно закону сохранения импульса:
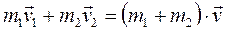, где 
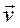- скорость тел после удара.
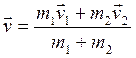(8)
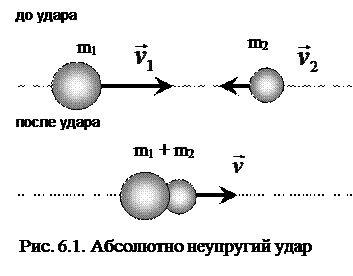
Если шары двигались навстречу друг другу, то вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий бóльшим импульсом. В частном случае, если массы шаров раны, то
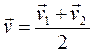при 
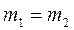(9)
В случае неупругого удара закон сохранения кинетической энергии не соблюдается. Вследствие удара происходит пластическая деформация тел и переход части механической энергии в тепловую или другие виды энергии.
Эту потерю можно оценить как разность кинетической энергии до и после удара:
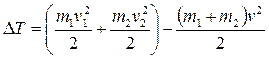подставим сюда (8):
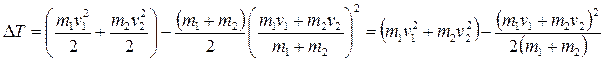
После преобразований получим выражение для потери кинетической энергии в результате абсолютно неупругого удара:
(10)
Если ударяемое тело было неподвижн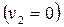о 
, то:
, 
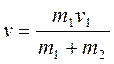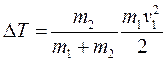(11,12)
Если 
, то 
и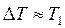 
, т.е. почти вся кинетическая энергия при неупругом ударе переходит в другие виды энергии. Поэтому для получения значительной деформации наковальня должна быть массивнее молотка.
ПРИМЕР:
Абсолютно упругий удар можно рассмотреть на примере установки, схема которой изображена на рисунке. Два шара массами m1 и m2 подвешены на расстоянии l от точки подвеса. Положения шаров в процессе эксперимента (до и после столкновения) определяются углами αi .
Применяя закон сохранения импульса к проекциям импульсов шаров на горизонтальное направление, получим для упругого удара соотношение:
,
учитывая, что шар m2 в начальном положении был неподвижен (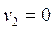 
):
,
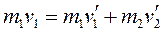или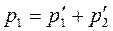 
| |
| |
В исходном положении шар 1 отклонен на угол α0, а его ц.м. поднят на высоту Δh0 . При этом потенциальная энергия шара меняется на величину
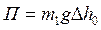
Если в системе нет потерь энергии, то при изменении угла от α0 до 0 кинетическая энергия шара 1 меняется от 0 до П:
,
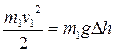откуда скорость в момент удара: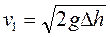 
.
Так, как 
, то окончательно формула для скорости шаров определится выражением:
,
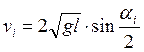тогда выражения для импульсов:
, 
, 
.
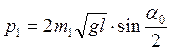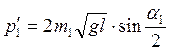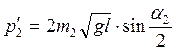Задавшись начальными условиями, найдем импульсы шаров после удара. Н.У.: m1 = 0,5кг; m2 = 0,2кг; l = 1м, 
.
1) Скорость первого шара до удара:
.
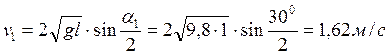2) Импульс первого шара до удара: 
.
Импульс второго шара до удара равен нулю, т.к. он покоится (v2 = 0).
3) Скорость 1-го шара после удара:
.
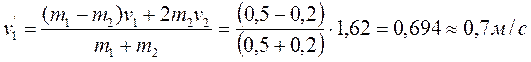4) Скорость 2-го шара после удара:
,
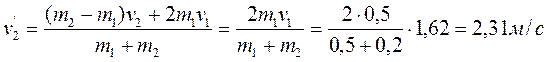5) Проверим закон сохранения импульса замкнутой механической системы:
, ч.т.д.
Дата добавления: 2014-12-20; просмотров: 8377;