Силы, действующие на механическую систему

В динамике, как и в статике, все силы делятся на активные или задаваемые и реакции связей или пассивные (ч. 1, п. 1.1.3). Кроме того, в динамике механической системы и твердого тела все силы делятся на внешние и внутренние.

Внешними называются силы, действующие на точки данной механической системы со стороны точек или тел, не входящих в данную систему, общепринятое обозначение - .

Внутренними называются силы, действующие на точки данной механической системы со стороны точек или тел данной системы, общепринятое обозначение - .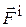

Деление сил на внешние и внутренние является условным. Все зависит от того, что выбрано за объект исследования, что принято за данную или рассматриваемую механическую систему. Например, объект исследования – двигатель внутреннего сгорания. Давление поршня на кривошип и давление кривошипа на поршень – внутренние силы. Те же силы будут внешними, если объект исследования – отдельно расматриваемый поршень или кривошип.

Из того, что внутренние силы возникают в механической системе попарно и на основании третьего закона динамики (п. 3.1.2) вытекают свойства внутренних сил механической системы:

1. Геометрическая сумма (или главный вектор) всех внутренних сил механической системы равен нулю: .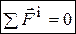

2. Геометрическая сумма моментов (или главный момент) всех внутренних сил механической системы относительно любого центра О равен нулю: .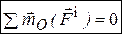

Но отсюда не следует, что внутренние силы механической системы взаимно уравновешиваются. Они приложены к разным точкам или телам системы и могут вызывать их относительные перемещения. Внутренние силы уравновешиваются только тогда, когда механическая система представляет собой абсолютно твердое тело.