Треугольные матрицы и характеристическое уравнение

Квадратная матрица, у которой все элементы, расположенные ниже или выше главной диагонали, равны нулю, называется треугольной. Треугольная матрица может быть верхнего и нижнего строения. Верхняя и нижняя формы имеют соответственно вид:

, .

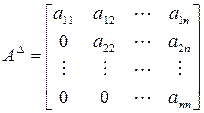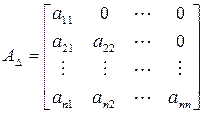Треугольные матрицы обладают рядом важных в практическом отношении свойств:

1) Определитель треугольной матрицы равен произведению ее диагональных элементов:

.

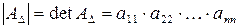Следовательно, треугольная матрица является неособенной только тогда, когда все элементы ее главной диагонали отличны от нуля.

2) Сумма и произведение треугольных матриц одинакового строения есть также треугольная матрица того же строения.

3) Неособенная треугольная матрица легко обращается, и ее обратная матрица снова имеет треугольную структуру того же строения.

4) Всякая неособенная матрица при помощи элементарных преобразований только над строками или только над столбцами может быть приведена к треугольной матрице. В качестве примера рассмотрим известную в теории устойчивости матрицу Гурвица

.

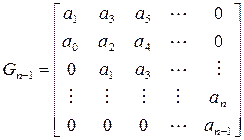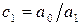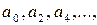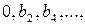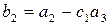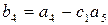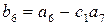Для перехода к верхнему треугольному виду проделаем следующие элементарные преобразования. Из каждого элемента второй строки вычтем стоящий над ним элемент первой строки, предварительно умноженный на . Вместо строки с элементами получим строку с элементами где , , , ... и т. д.

Выполним аналогичные операции в остальных нижележащих строках. Затем вычтем из каждого элемента третьей строки преобразованной матрицы стоящие над ней элементы строки, умноженные на 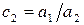, и повторим аналогичные операции в остальных строках. Продолжим процесс по этой процедуре до тех пор, пока на m-м шаге не получим верхнюю треугольную матрицу

.

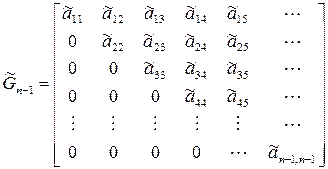Такие преобразования по существу эквивалентны умножению матрицы справа (или слева) на некоторую другую вспомогательную матрицу.

Определитель матрицы Гурвица

.

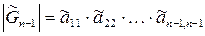Существует теорема о разложении любой квадратной матрицы в произведение двух треугольных. Согласно этой теореме, всякая квадратная матрица может быть представлена в виде произведения нижней и верхней треугольных матриц:

,

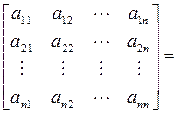
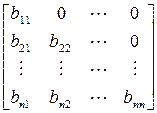
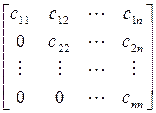при условии, что ее диагональные миноры отличны от нуля:

, , .

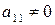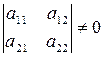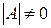Это разложение является единственным, если зафиксировать диагональные элементы одной из треугольных матриц (например, положить их равными единице). Разложение любой квадратной матрицы в произведение двух треугольных с предписанными диагональными элементами широко используется в вычислительных методах при решении задач с помощью ЭВМ.

Однозначное представление матрицы в виде произведения двух треугольных может быть обобщено на клеточные матрицы. В таких матрицах сами элементы являются матрицами. При этом матрица может быть разложена в произведение нижней и верхней квазитреугольных матриц.

Определитель квазитреугольной матрицы равен произведению ее диагональных клеток.

В отличие от диагональных матриц операция умножения треугольных матриц в общем случае не коммутативна.

В вычислительных методах теории управления существенную роль играют не только треугольные, но и так называемые почти треугольные матрицы. Многие методы используют разложение матрицы в виде произведения двух матриц, одна из которых имеет треугольное строение. Матрица А называется правой (левой) почти треугольной или матрицей Хессенберга, если для ее элементов а_ij выполняются соотношения:

; ; .

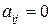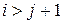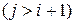Например, матрица Хессенберга правой почти треугольной формы размерности (4x4) имеет вид

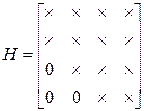
Отметим полезные особенности рассматриваемых матриц, которые используются в вычислительных методах:

а) сумма почти треугольных матриц одинакового строения будет треугольной матрицей того же строения, а произведение - нет;

б) построение характеристического полинома почти треугольных матриц экономично, так как требует гораздо меньшего объема вычислений, чем при произвольной форме матрицы. Число операций умножений составляет 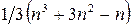, сложений - ;

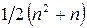в) почти треугольная матрица может быть разложена в произведение двух треугольных, причем в разложении одна из матриц будет иметь более простую структуру, а именно, будет двухдиагональной.

В современных инженерных методах, заложенных в системы автоматизированного проектирования, широко используется мультипликативное представление матриц, например, QR-представление. Его сущность состоит в том, что любую квадратную матрицу А можно представить в виде произведения ортогональной и почти треугольной форм

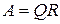, или 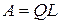, (4.4)

где Q - ортогональная матрица; R - правая (верхняя) треугольная форма; L - левая (нижняя) треугольная форма матрицы.

Представление (4.4) называется QR-разложением (в случае нижней треугольной матрицы QL-разложением) и для матрицы А является единственным.

QR- и QL-алгоритмы принципиально мало различаются. Их использование зависит от того, как расположены элементы матрицы. Если они сосредоточены в нижнем правом углу, эффективнее использовать QL-алгоритм. Если элементы матрицы сосредоточены в левой верхней части, то целесообразнее использовать QR-алгоритм. При правильной реализации на ЭВМ ошибки округления во многих случаях не оказывают большого влияния на точность вычисления.