Матричная запись системы линейных алгебраических уравнений

Система n алгебраических уравнений с n неизвестными вида

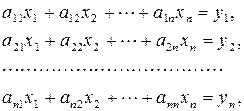(4.1)

отражает зависимость между переменным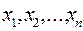и и 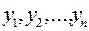. Эта зависимость определяется линейным преобразованием переменных х в переменные у с помощью элементов матрицы

.

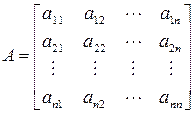Система (1) может быть записана в виде одного матричного уравнения

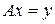, (4.2)

где х - вектор-столбец, элементами которого являются зна­чения неизвестных 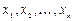; y-вектор-столбец свободных членов. Уравнение (4.2) можно рассматривать как преобразование заданного вектора х в новый вектор у посредством матрицы А. Иначе говоря, матрица А ставит в соответствие данному вектору х новый вектор у.

Если матрица А неособенная, то решение системы сразу получается путем умножения (4.2) слева на :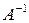

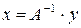(4.3)

Формула (4.3) представляет собой матричный вариант известных формул Крамера.

Контрольные вопросы

1) Какая таблица называется матрицей?

2) Какие виды матриц существуют?

3) Как вычисляется обратная матрица?

4) Как перемножаются матрицы?

5) Как при помощи матриц записывается система алгебраических уравнений?