Произведение матриц

Под произведением двух матриц А и В понимается матрица С = АВ, элементы которой определяются путем умножения i-й строки первой матрицы на j-и столбец второй матрицы и полученные произведения складываются. Таким образом,

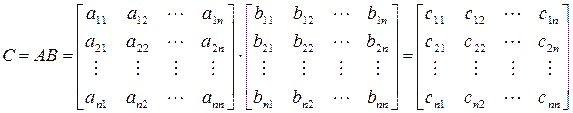
где ,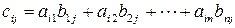

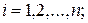
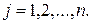
Процесс формирования произведения для быстрого запоминания можно облечь в следующую схему. Для иллюстрации рассмотрим перемножение двух матриц размерности 3×3.

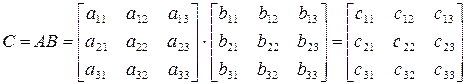
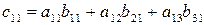
Первая строка умножается на первый столбец. Результат перемножения складывается. Образуется элемент матрицы с₁₁.

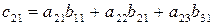
Вторая строка умножается на первый столбец. Результат перемножения складывается. Образуется второй элемент первого столбца с₂₁.

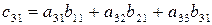
Третья строка умножается на первый столбец. Результат умножения складывается, образуя последний элемент c₃₁ первого столбца.

Операции по формированию элементов второго и третьего столбцов выполняются аналогично.

, , , , , .

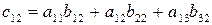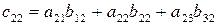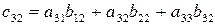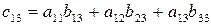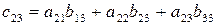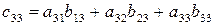Произведение матриц А и В имеет смысл только в предположении, что число столбцов „матрицы А равно числу строк матрицы В. По этой причине произведение прямоугольной матрицы на вектор-столбец есть вектор-столбец. произведение вектор - строки на вектор-столбец есть матрица, состоящая из одного элемента.

Обычная скалярная алгебра подчиняется шести с законам:

1) Закон коммутативности сложения:

.

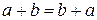2) Закон ассоциативности сложения:

.

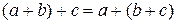3) Закон коммутативности умножения:

.

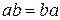4) Закон ассоциативности умножения:

.

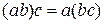5) Закон дистрибутивности умножения:

, ;

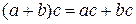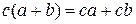6) Неразложимость нуля на множители, отличные от нуля: если 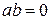, то либо 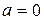, либо 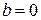, либо .

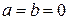В операциях с матрицами законы 1, 2, 4 и 5 выполняются всегда. Однако законы 3 и 6 не соблюдаются. Закон 3 нарушается в силу того, что при перемножении матриц строки первой матрицы комбинируются со столбцами второй матрицы по изложенному выше правилу несимметрично. Такое несимметричное «перемешивание» элементов перемножаемых матриц между собой приводит к тому, что в общем случае

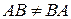
В тех случаях, когда операция умножения коммутативна, т. е. 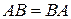, матрицы называются коммутативными (иногда коммутирующими) или перестановочными. Например, диагональные матрицы при умножении всегда коммутируют между собой, причем произведение диагональных матриц, в свою очередь, также является диагональной матрицей.

Скалярная матрица коммутирует с любой квадратной матрицей одинакового порядка. Это же свойство относится и к единичной матрице Е. Она выполняет такую же роль, как единица среди обычных скалярных величин:

, .

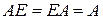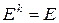Кроме того, всегда соблюдается равенство

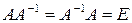
Каждая матрица коммутирует сама с собой и со своей произвольной целой положительной степенью.

Если производится умножение матрицы А слева на некоторую диагональную матрицу D, это соответствует операциям со строками, если умножение выполняется справа, - со столбцами.

Пример 4.1. Умножение матрицы А слева на диагональную матрицу D эквивалентно умножению каждой строки матрицы А на соответствующий диагональный элемент:

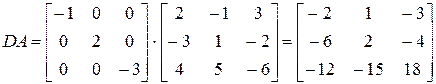
Пример 4.2. Умножение справа на D сводится к умножению элементов каждого столбца на соответствующий элемент диагонали:

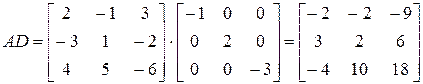
Пример 4.3. Коммутируемость диагональных матриц:

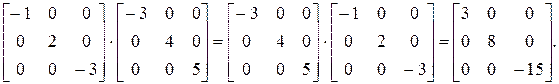
Скалярная матрица (матрица, у которой диагональные элементы равны между собой) равна произведению единичной матрицы на скалярную величину. В качестве примера перемножим две скалярные матрицы:

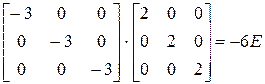
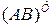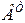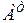Справедливо следующее правило транспонирования произведения. Транспонированное произведение матриц равно произведению двух транспонированных матриц и , перемноженных в обратной последовательности:

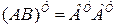
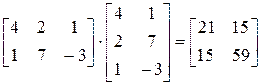
Произведение любой матрицы на свою транспонированную является симметрической матрицей. Например,

Следовательно, если А - симметрическая матрица, то матрица 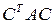- также симметрическая.

Произведение обратных матриц подчиняется тому же свойству перестановки сомножителей, что и произведение транспонированных матриц, а именно

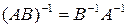
Определитель произведения двух квадратных матриц равен произведению определителей перемножаемых матриц:

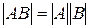
При образовании произведения нескольких матриц множители в силу ассоциативности закона умножения можно группировать как угодно, при условии, что порядок перемножения сомножителей не нарушается.

При умножении матрицы ранга r на неособенную справа или слева ранг произведения остается равным r.