Нормальные и совершенные нормальные формы логических функций

Конъюнкция (дизъюнкция), в которой каждая переменная с инверсией или без встречается не более одного раза, называется элементарной. Число входящих в нее переменных определяет ранг конъюнкции (дизъюнкции).

Дизъюнкция любого числа элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ), например:

.

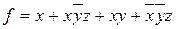Конъюнкция любого числа элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ). Например:

.

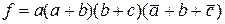Для каждой функции может существовать несколько равносильных ДНФ (или КНФ), например:

.

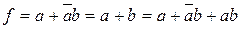ДНФ (КНФ), содержащая наименьшее число переменных по сравнению с другими равносильными ДНФ (КНФ), называется минимальной.

ДНФ логической функции, состоящая из элементарных конъюнкций одинакового ранга, называется совершенной дизъюнктивной нормальной формой (СДНФ). В СДНФ каждая элементарная конъюнкция включает все переменные с инверсиями или без, причем одинаковых конъюнкций нет, например:

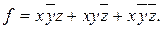
От любой ДНФ можно перейти к СДНФ. Для этого необходимо:

- вести недостающие переменные в конъюнкции младших рангов умножением их на равносильность вида формула (х - недостающая переменная);

- раскрыть скобки и избавиться от повторяющихся конъюнкций в соответствии с правилом х+х=х.

Пример 3.4. Для функции 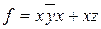составить СДНФ

.

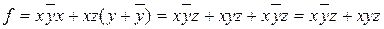СДНФ обладает следующими свойствами:

- если при каком-то наборе f = 1, то СДНФ только одна из элементарных конъюнкций принимает значение единицы;

- если для данного набора f = 0, то в СДНФ ни один из членов не будет равен единице.

Элементарные конъюнкции, входящие в СДНФ, называют минтермами, или конституентами единицы, поскольку каждая из них соответствует одному из наборов, при котором f= 1. Таким образом, СДНФ есть дизъюнкция конституентов единицы тех наборов переменных, на которых данная функция равна единице, Из этого следует, что по заданной таблице истинности может быть составлена СДНФ функции, содержащая столько членов, сколько единичных значений принимает функция.

Пример 3.5. Построить СДНФ функции, таблица истинности которой имеет вид (таблица3.2):

.

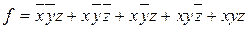По аналогии с дизъюнктивными формами КНФ логической функции, состоящая из элементарных дизъюнкций одинакового ранга, называется совершенной конъюнктивной нормальной формой. (СКНФ).

Свойства СКНФ:

- если для данного набора f=0, то в СКНФ только одна из элементарных конъюнкций принимает нулевое значение;

- если для данного набора f=1, то в СКНФ ни один из членов не принимает нулевое значения.

СКНФ является конъюнкцией макстермов, или конституентов нуля тех наборов, на которых данная равна нулю. Правило построения конституентов нуля: каждая переменная входит в конституент без инверсии, если значение ее в данном наборе равно 0, или с инверсией, если значение ее равно 1.

Пример 3.6 Составить СКНФ функции, заданной в примере 3.5. Функция принимает нулевое принимает нулевое значение на трех наборах. Следовательно, в СКНФ входят три конституенты нуля, т.е.

.

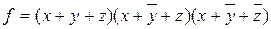СДНФ и СКНФ, представляющие собой суперпозицию минтермов или макстермов, называют каноническими формами логических функций. Для равносильных функций их СДНФ (СКНФ) совпадают. Проверка такого совпадения является одним из метолов доказательства равносильности функций.