Основные логические операции
Наиболее употребительными логическими операциями является логические операции отрицание, сложение и умножение. Они позволяют составить любую логическую функцию. Рассмотрим операцию отрицание. Если для  множеством истинности является
множеством истинности является 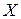 . То через
. То через 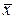 обозначается высказывание с множеством истинности, заштрихованным на рисунке 3.1.а., функция
обозначается высказывание с множеством истинности, заштрихованным на рисунке 3.1.а., функция 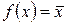 (читается «не
(читается «не  ») называется функцией НЕ, или инверсией. Из таблицы истинности, представленной на рисунке 3.1.б следует что
») называется функцией НЕ, или инверсией. Из таблицы истинности, представленной на рисунке 3.1.б следует что 
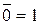 и
и 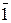 = 0. Изображается функция
= 0. Изображается функция 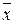 в виде логического элемента, называемого элементом НЕ, или инвертором представленного на рисунке 3.2 в.
в виде логического элемента, называемого элементом НЕ, или инвертором представленного на рисунке 3.2 в.
 |
 Логическое сложение обозначается знаком + или логическим символом V. Функция
Логическое сложение обозначается знаком + или логическим символом V. Функция 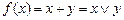 , имеет множество истинности
, имеет множество истинности 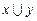 и получила название функции ИЛИ (дизъюнкции). Диаграмма, соответствующая функции х+у, и таблица истинности приведены на рисунках 3.2, а, б.
и получила название функции ИЛИ (дизъюнкции). Диаграмма, соответствующая функции х+у, и таблица истинности приведены на рисунках 3.2, а, б.
С помощью диаграммы можно убедиться в справедливости следующего тождеств:
1) x+1=1, (x 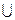 I=I),
I=I),
2) x+0=x, (x 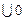 =x),
=x),
3) 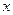 +
+ 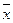 =1, (
=1, ( 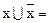 I),
I),
4) x+x=x (x 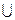 x=x).
x=x).
Из последнего тождества следует , что в функциях логического сложения отсутствуют коэффициенты.
Логический элемент (рисунок 3.2 в) называет элементом ИЛИ (лизъюнктором).
Логическое умножение соответствует операция пересечения множеств. Функция
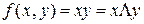 .
.
Следующий 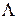 - символ логического умножения, называется функцией И, или конъюнкцией. Множество истинности Х
- символ логического умножения, называется функцией И, или конъюнкцией. Множество истинности Х 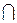 У и таблица истинности показаны на рисунках 3.3 а, б.
У и таблица истинности показаны на рисунках 3.3 а, б.
Для функции ху определены тождества:
1) x1=x (x 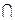 I=x),
I=x),
2) x0=0 (x 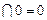 ),
),
3) 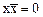 , (x
, (x  x=
x=  ),
),
4) xx=x (x  x=x).
x=x).
Последнее тождество показывает, что в алгебре логики отсутствует возведение в степень.
Соответствующий логический элемент (рисунок 3.3в) называется элементом И (конъюнктором), а также схемой совпадения.
Операции логического сложения и логического умножения возможны для трех и более переменных.
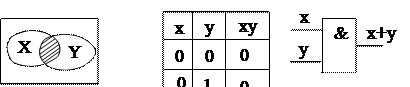 |
Дата добавления: 2014-12-27; просмотров: 1257;
