Действия над графами
Над графами представляющими бинарные отношения на множестве, можно выполнять операции объединения, пересечения, произведения (композиции), декартово произведения и других. Рассмотрим некоторые операции.
Объединение графов 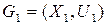 и
и 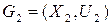 называют граф
называют граф 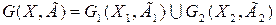 , у которого множество вершин определяется объединением вершин
, у которого множество вершин определяется объединением вершин 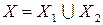 , а отображения каждой вершины – объединением отображений соответствующих вершин, то есть
, а отображения каждой вершины – объединением отображений соответствующих вершин, то есть 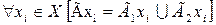 .
.
Пример 2.1 Рассмотрим выполнение операции объединения графов изображенных на рисунках 2.7а и 2.7б.
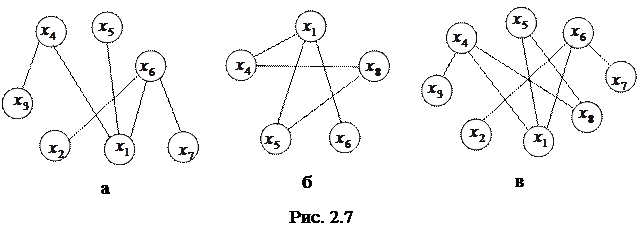
Для выполнения объединения графов необходимо вначале выполнить операцию объединения вершин графов:
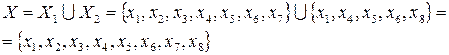 .
.
 |
Теперь определим отображения каждой вершины объединенного графа:
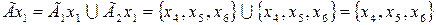 ,
, 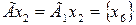 ,
, 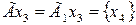 ,
, 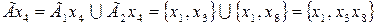 ,
, 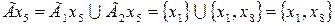 ,
,
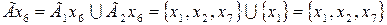 ,
, 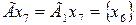 ,
, 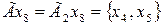 .
.
В результате по этим данным получим граф изображенный на рисунке 2.7в. Аналогично определяется объединение нескольких графов:
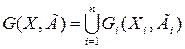 .
.
В результате пересечения двух графов получим граф, вида:
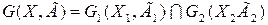 .
.
Результирующий граф имеет вершины, которые получаются в результате пересечения вершин исходных графов:
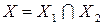 ,
,
а отображение каждой вершины поученного в результате пересечения графа определяется следующим образом:
 .
.
Пример 2.2. В результате пересечения графов изображенных на рисунке 2.7а и 2.7б, получим граф, вершины которого определяются как результат пересечения вершин исходных графов:
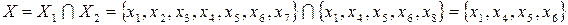 .
.
Отображение каждой вершины результирующего графа определяются из выражения вида:
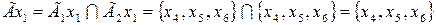 ,
, 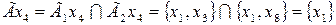 ,
, 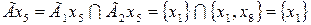 ,
, 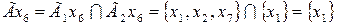 .
.
 По этим данным построим результирующий граф, который представлен на рисунке 2.8. Подобным образом можно выполнить операцию пересечения нескольких графов:
По этим данным построим результирующий граф, который представлен на рисунке 2.8. Подобным образом можно выполнить операцию пересечения нескольких графов: 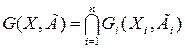 .
.
Раскраской вершин графа 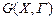 называют разбиение вершин на k подмножеств
называют разбиение вершин на k подмножеств 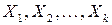 , при котором никакие две вершины одного и того же подмножества не являются смежными. Если вершины каждого подмножества окрасить в один цвет, то никакое ребро графа не будет инцидентно вершинам, окрашенным в одинаковый цвет. Такой граф называют k-хроматическим графом, а наименьшее число подмножеств, на которое разбивается граф – хроматическим числом графа
, при котором никакие две вершины одного и того же подмножества не являются смежными. Если вершины каждого подмножества окрасить в один цвет, то никакое ребро графа не будет инцидентно вершинам, окрашенным в одинаковый цвет. Такой граф называют k-хроматическим графом, а наименьшее число подмножеств, на которое разбивается граф – хроматическим числом графа 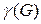 .
.
Важное практическое применение имеют двудольные, или бихроматические графы с 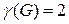 . Такой граф обозначают
. Такой граф обозначают 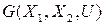 , где U – ребра, соединяющие подмножества вершин
, где U – ребра, соединяющие подмножества вершин 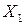 и
и 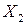 . Граф
. Граф 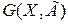 , изображенный на рисунке 2.7в, относится к двудольным и может быть представлен, как показано на рисунке 2.9. Условие бихроматичности графа – отсутствие элементарных циклов нечетной длины. Если для произвольного неорграфа условие бихроматичности не выполняется, из него можно выделить удалением некоторых ребер суграф, являющийся двудольной частью. При этом суграф с наибольшим числом ребер будет называться максимальной двудольной частью неорграфа.
, изображенный на рисунке 2.7в, относится к двудольным и может быть представлен, как показано на рисунке 2.9. Условие бихроматичности графа – отсутствие элементарных циклов нечетной длины. Если для произвольного неорграфа условие бихроматичности не выполняется, из него можно выделить удалением некоторых ребер суграф, являющийся двудольной частью. При этом суграф с наибольшим числом ребер будет называться максимальной двудольной частью неорграфа.
Контрольные вопросы
1) В каком случае граф называется связным?
2) Какие графы называются деревом, лесом?
3) Как выполняется операция объединения графов?
4) Как выполняется операция пересечения графов?
5) Какие графы называются бихроматическими?
Дата добавления: 2014-12-27; просмотров: 2131;
