Матричное представление графов
Любой граф, заданный множествами Х и Г или в виде рисунка, может быть также представлен с помощью матриц смежности и инцидентности.
В квадратной матрице смежности  строки и столбцы соответствуют вершинам графа. Для орграфа на пересечении i-той строки и j-того столбца матрицы значения элементов образуются по правилу
строки и столбцы соответствуют вершинам графа. Для орграфа на пересечении i-той строки и j-того столбца матрицы значения элементов образуются по правилу
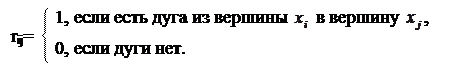 |
 Для графа на рисунке 2.2 матрица смежности имеет вид:
Для графа на рисунке 2.2 матрица смежности имеет вид:
Единицы в главной диагонали матрицы свидетельствуют о наличии петель в графе.
Для неорграфа в матрице смежности на пересечении строк и столбцов стоят единицы, если вершины соединены ребрами. Матрица, построенная по этому правилу для графа на рисунке 2.3 имеет вид
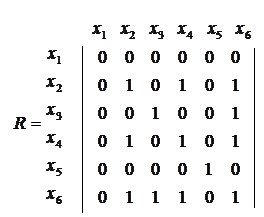 |
или соответствует ранее построенной матрице отношений в примере 1.16. Поскольку отношения в неорграфе обладают свойством симметрии  . Следовательно, все ребра определяются верхним правым треугольником матрицы, включающим диагональ. Поэтому для задания неорграфа можно использовать треугольную матрицу.
. Следовательно, все ребра определяются верхним правым треугольником матрицы, включающим диагональ. Поэтому для задания неорграфа можно использовать треугольную матрицу.
Существуют разновидности матриц смежности. В матрице весовых соотношений элемент  вместо 1 принимает значения веса связи
вместо 1 принимает значения веса связи 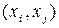 , в матрице длин – длины ребра или дуги
, в матрице длин – длины ребра или дуги 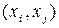 .
.
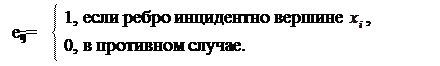 В прямоугольной матрице инцидентности
В прямоугольной матрице инцидентности  строки соответствуют вершинам графа, а столбцы – ребрам (дугам). Для неорграфа на пересечении i-той строки и j-того столбца элементы матрицы образуются по следующему правилу
строки соответствуют вершинам графа, а столбцы – ребрам (дугам). Для неорграфа на пересечении i-той строки и j-того столбца элементы матрицы образуются по следующему правилу
 Для графа, изображенного на рисунке 2.1в, матрица инцидентности имеет вид
Для графа, изображенного на рисунке 2.1в, матрица инцидентности имеет вид
В каждом столбце матрицы Е не более двух единиц, поскольку каждое ребро соединяет две вершины. Столбцы, соответствующие петлям, содержат по одной единице.
Для орграфа в матрицу инцидентности заносится
 |
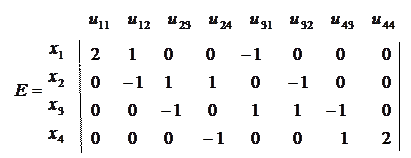 Для графа на рисунке 2.2 матрица инцидентности записывается в виде:
Для графа на рисунке 2.2 матрица инцидентности записывается в виде:
Матрица инцидентности, как и матрица смежности, однозначно определяет граф. Существуют приемы перехода от одной матрицы к другой.
С помощью матриц смежности можно установить изоморфизм графов. Для этого необходимо в матрице смежности одного графа проделать перестановки строк и столбцов. Если после очередной перестановки получим матрицу, тождественно совпадающую с матрицей другого графа, то графы изоморфны.
Помимо рассмотренных матриц, для описания графов используются матрицы контуров, расстояний и другие.
Контрольные вопросы
1) Из каких элементов состоит граф?
2) Какие различия имеются между ориентированным и неориентированным графами?
3) Как формируются матрицы смежности ориентированных и неориентированных графов?
4) Как формируются матрицы инцидентности ориентированных и неориентированных графов?
Дата добавления: 2014-12-27; просмотров: 4533;
