Логические функции и способы их представления

Составной частью математической логики является учение о высказываниях. Примем множество электроизмерительных приборов за некоторое универсальное множество I. Элементы I могут быть сгруппированы по различным частным признакам в подмножества: А – подмножество амперметров, В - вольтметры, С - магнитоэлектрические приборы, D - цифровые приборы и т.п. Сообщение типа «этот прибор является вольтметром» оказывается истинным, если данный прибор относится к подмножеству В, и ложным, если не относится. Каждое подобное утверждение, которое может быть либо истинным, либо ложным, называют высказыванием. А множество, для элементов которого высказывание оказывается истинным, называется множеством истинности данного высказывания.

Высказывания, которым соответствуют простые множества истинности (например А, В,…), называются простыми высказываниями. Но множество истинности может оказаться и сложным, например 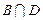. В этом случае имеем составное высказывание, в котором два простых высказывания объединены логической связкой «и» («этот прибор цифровой и является вольтметром»).

Можно отвлечься от смыслового содержания и рассматривать простые высказывания как величины, принимающие значения «истинно» или «ложно». Тогда с помощью определенных действий называемых логическими операциями, можно получать из исходных высказываний новые простые или составные высказывания.

Совокупность множества элементов (высказываний), логических операций, ряда определенных правил и законов получила название алгебра логики, являющейся одной из разновидности булевой алгебры (по имени английского математика Джорджа Буля).

Высказывания, которые могут принимать только два значения «истинно» или «ложно», в алгебре логики называются логическими переменными. Обозначаются они строчными буквами латинского алфавита а, в, с,…х, у, z с индексами или без индексов. Значения «истинно» и «ложно» обозначают 1 и 0.

Операция над логическими переменными приводят к появлению нового высказывания, которое также будет принимать одно из двух значений – 0 или 1. Предположим, что имеется некоторое множество переменных 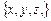. Результат логической операции может оказаться равным при различных значениях переменных. Если назовем комбинацию значений переменных набором, то налицо однозначное отображение множество наборов в множество результатов 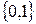, что характеризует функциональную зависимость. Функция f(x,y,z), которая, как и ее аргументы (логические переменные), может принимать только два значения – 0 или 1 называется логической или булевой функцией. По числу переменных различают логические функции одной, двух и многих переменных.

Как указывалось ранее, функция может быть представлена таблицей, формулой или графиком. Чтобы задать логическую функцию, достаточно указать ее значения для всех наборов переменных, составив таблицу истинности. Функция может быть задана формулой, указывающей последовательности логических операций над переменными. Что касается графика, то для логической функций он не строится, так как наборы значений аргументов, изображаемые в виде вершин единоличного 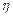- мерного куба, неудобны для графического моделирования функции. Тем не менее, графическое пояснение логической функции возможно.

Поскольку между высказываниями и множествами имеется тесная смысловая связь, логические операции могут быть определены через соответствующие операции алгебры множеств. Тогда полученную в результате логическую функцию можно представить графически множеством истинности в виде диаграммы Эйлера–Венна.

Функция может быть также представлена логической схемой - условным графическим изображением логической операции в виде одного или нескольких типовых логических элементов.