Разновидности графов и выполнение операций с графами

Граф, у которого хотя бы одна пара вершин соединена несколькими ребрами (дугами в одном направлении), называют мультиграфом. Ребра (дуги), связывающие одну и ту же пару вершин называют кратными.

Граф, не имеющий ребер и состоящий из изолированных вершин называется нуль-графом.

Число ребер, инцидентных одной вершине неорграфа, называют локальной степенью вершины - 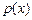. Неорграф, у котрого

,

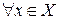
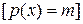то есть все вершины имеют одинаковую степень m, называется однородным степени m. В орграфе число исходящих дуг определяет полустепень исхода 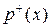, а число заходящих дуг – полустепень захода вершины 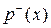. Если

,

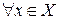
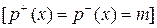то орграф также считается однородным степени m. Петля при определении степени вершины считается дважды: как исходящая дуга и как заходящая. Граф на рисунке 2.2 является примером однородного графа степени два.

Граф, все вершины которого попарно смежны, то есть между любой парой вершин имеется ребро, называется полным. Полный граф с m вершинами является одновременно и однородным степени m-1, поскольку каждая вершина соединена с m-1 остальными.

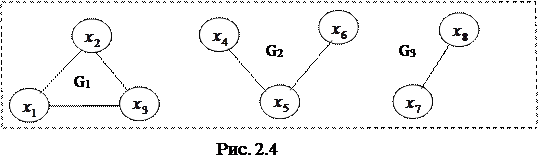
Если любые две вершины связаны цепью, граф называют связным. При определении связности орграфа можно не принмать во внимание направленность дуг. Если же для любой пары вершин найдется соединящий их путь (с учетом направленности дуг), то орграф считается связным. Графы, не отвечающие условию связности, состоят из связных подграфов, которые называются компонентами связности. На рисунке 2.4 приведен граф, состоящий из трех компонент связности.

Разновидностями связных графов являются эйлеровы и гамильтоновы графы. В первом имеется элементарный цикл, который включает все ребра, проходя через каждое ребро только один раз, и называется эйлеровым циклом. Во втором имеется гамильтонов цикл, проходящий через каждую вершину графа один раз.

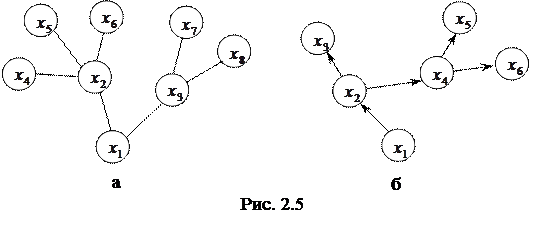
К связным графам относятся также деревья. Деревом называют конечный связный неорграф, не содержащий циклов (рисунок 2.5а). Вершина 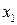является корнем дерева, а другие вершины с локальной степенью 1 называются концевыми 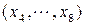. Связный орграф без петель с корнем 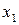и остальными вершинами, в каждую из которых заходит только одна дуга, называется прадеревом (рисунок 2.5б).

Несвязный граф без циклов называется лесом. Компонентами связности леса могут быть деревья, а также отдельные ребра и изолированные вершины, являющиеся частным случаем деревьев. На рисунке 2.6 показан пример такого графа.

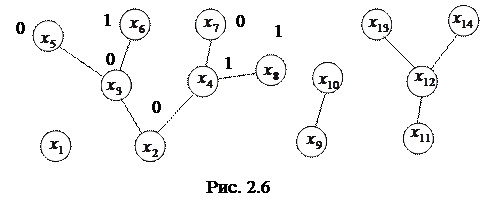Если пометить вершины одного из деревьев нулями и единицами, как показано на рисунке 2.6, то записав пути от корня до концевых вершин, получим комбинации 000, 001, 010, 011.

Дерево, являющееся частичным графом графа , называется деревом покрывающим граф G. На рисунке 2.3б жирными линиями выделено такое дерево. Наименьшее число ребер, которые надо удалить из графа, чтобы он стал ациклическим (то есть не содержащим циклов), определяется цикломатическим число графа. Если граф имеет n вершин, m ребер и k компонент связности, то его цикломатическое число равно

.

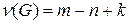Для графа на рисунке 2.3б для получения покрывающего дерева необходимо удалить 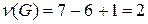ребра.