Анализ трудоемкости операций над рассеянной таблицей
Пусть для хранения таблицы отведено m позиций, и в таблице имеется n записей, тогда a=n/m £ 1 – коэффициент загруженности памяти. Вероятность того, что хеш-адрес попадет в занятую позицию равна a, а в свободную 1-a. При вставке нам удастся найти место для новой записи:
- с 1-й попытки с вероятностью 1-a,
- со 2-й попытки – с вероятностью a(1-a) (первая попытка неудачная, вторая успешная),
- c 3-й попытки – с вероятностью a2(1-a) (две первых неудачны, третья успешна) и т.д.
Математическое ожидание числа попыток N при вставке:
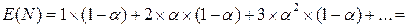
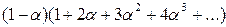 (13)
(13)
Выражение 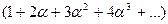 является производной по a от суммы геометрической прогрессии
является производной по a от суммы геометрической прогрессии 
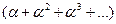 , которая может быть вычислена по формуле (a+a2+a3+…)=a /(1-a) (14),
, которая может быть вычислена по формуле (a+a2+a3+…)=a /(1-a) (14),
Подставляя производную правой части (14) в (13), получим:
E(N)=1/ (1-a) (15)
Для определения среднего числа проб при поиске заметим, что запись будет найдена в точности за столько же проб, сколько потребовалось при ее вставке. Каждая запись вставляется при своем значении a, так, например, при вставке первой записи a=0. Усредняя (14) по a, получим:
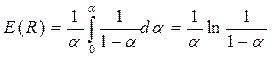 (16)
(16)
Таблица, приведенная ниже, дает представление о среднем числе проб при вставке и поиске.
| a | N(a) | R(a) |
| 0,20 | 1,25 | 1,12 |
| 0,50 | 2,00 | 1,39 |
| 0,80 | 5,00 | 2,01 |
| 0,90 | 10,00 | 2,56 |
| 0,95 | 20,00 | 3,15 |
| 0,99 | 100,00 | 4,65 |
Как видно из таблицы, не следует рассчитывать на полное использование памяти. Для динамичных таблиц коэффициент загрузки памяти не должен превышать 0,7 – 0,8.
Контрольные вопросы
1) В чем заключается основное отличие рассеянных таблиц от таблиц с прямым доступом?
2) Каким требованиям должны удовлетворять первичная и вторичная хеш-функции?
3) Какие методы разрешения коллизий в рассеянных таблицах вы знаете?
4) В чем заключается явление скучивания?
5) Опишите алгоритмы поиска, вставки и удаления для метода открытой адресации.
6) Дайте оценку трудоёмкости операций поиска и вставки для рассеянной таблицы.
Литература
1. Вирт Н. Алгоритмы и структуры данных. СПб Невский диалект 2001г. 352 с.
2.Ахо А., Хопкрофт Д, Ульман Дж.., Структуры данных и алгоритмы СПб Издательский дом "Вильямc", 2000 г., 384 с.
3.Мейн М. Савитч У. Структуры данных и другие объекты в C++, 2-е издание. СПб Издательский дом "Вильямс" 2002г. 832 с.
4.Гудрич М.Т., Тамассия Р. Структуры данных и алгоритмы в Java. СПб Издательский дом "Вильямс" 671 с.
5.Бакнелл Дж. Фундаментальные алгоритмы и структуры данных в Delphi. М. ДиаСофт. 560 с.
Дата добавления: 2014-12-02; просмотров: 1529;
