Удаление

Если удаляемый ключ находится в листе и после удаления число ключей в узле не становится меньше (m-1)/2, то ключ просто удаляется из узла и на этом операция заканчивается.

Если ключ находится не в листе, то вместо него удалим последователя в обратном порядке (а он всегда в листе), а затем вернем на место ключа, который действительно надо было удалить. Алгоритм определения последователя ключа из нелистового узла следующий:

- спуститься вниз по указателю справа от ключа

- далее спускаться по самым левым связям до листа

Так или иначе, в некотором листе станет на один ключ меньше. Ситуацию, когда число ключей становится меньше (m-1)/2, назовем антипереполнением. Антипереполнение должно быть ликвиди­ро­вано. Для этого поищем "богатого" соседа, у которого можно было бы "занять" ключи. Если такой сосед найдется, то поступим так же, как и при ликвидации переполнения. Рассмотрим множество ключей, состоящее из ключей соседа, разделяющего ключа в отце и ключей узла, в котором произошло антипереполнение. Средний ключ поместим в отца, а оставшиеся ключи поделим пополам между узлом, в котором произошло антипереполнение и соседом. Рис. 51 иллюстрирует ситуацию.

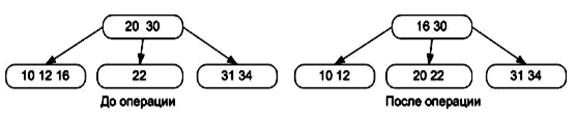
Рис.51 Ликвидация антипереполнения

Если же подходящего соседа не найдется, то выбирается любой из соседей, и удаляется, а ключи, составляющие описанное выше множество, помещаются в узел, вызвавший антипереполнение (рис.52).

Рис.52 Слияние узлов при ликвидации антипереполнения

В результате слияния число ключей в отце уменьшается на единицу и может вызвать его антипереполнение, которое обрабатывается точно также. Процесс может рекурсивно подняться до корня и уничтожить его. В этом случае корневым узлом становится результат последнего слияния.