II. Анализ на чувствительность модели к изменениям правых частей ограничений .

Из теоремы об оценках известно, что изменение правых частей ограничений 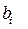приводит к увеличению или уменьшению значения целевой функции 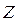. Найдем такие интервалы изменения каждого из свободных членов 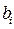системы ограничений исходной задачи, в которых оптимальный план двойственной задачи не менялся бы, то есть найдем интервалы устойчивости (неизменности) двойственных оценок по отношению к изменениям запасов ресурсов каждого вида.

Известно, что двойственные оценки не меняют своей величины, если не меняется набор переменных, входящих в базис оптимального решения, тогда как значения неизвестных в оптимальном решении могут меняться.

Рассмотрим модель исходной задачи линейного программирования (1.6.1.1) в матричной форме:

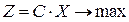
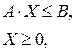
где 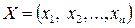- вектор неизвестных;

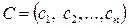- вектор коэффициентов при неизвестных в целевой функции;

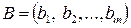- вектор свободных членов ограничений исходной задачи;

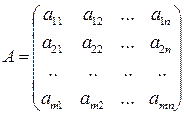- матрица коэффициентов в системе ограничений.

После приведения задачи линейного программирования к канонической форме введением дополнительных неизвестных задача примет вид:

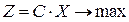
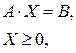
где вектор неизвестных переменных 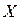теперь имеет размерность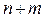 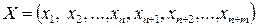. Размерность матрицы А также изменится и будет равна .

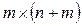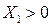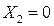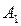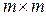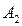В результате решения задачи линейного программирования вектор X разобьется на два подвектора: - неизвестные, вошедшие в базис оптимального решения и - свободные переменные. Соответственно и матрица А разобьется на две подматрицы (размерности ) и (размерности 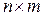). 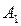состоит из столбцов матрицы А, соответствующих ненулевым переменным в оптимальном решении.

Тогда 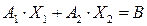. Так как 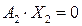, то 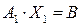. Решение такого матричного уравнения находится из уравнения 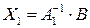. Обозначим 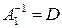, тогда 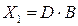, где матрица 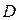характеризует влияние ресурсов на величину выпуска продукции .

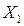Если изменим запасы ресурсов ( 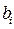), то есть дадим 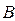приращение 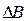, тогда уравнение 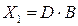примет вид: 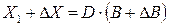, или 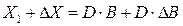. Так как 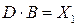, то последнее равенство примет вид: .

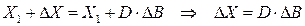Равенство 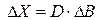определяет величину структурных сдвигов в выпуске продукции при изменении ограничений исходной задачи. Любое изменение исходных данных прямой задачи может оказать влияние, как на ее оптимальный план ( 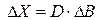), так и на систему оптимальных двойственных оценок. Поэтому чтобы проводить экономический анализ с использованием двойственных оценок, нужно знать их интервал устойчивости.

Следовательно, необходимо определить такие интервалы изменения каждого из свободных членов системы линейных уравнений 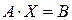, в которых оптимальный план двойственной задачи не меняется. Это имеет место тогда, когда среди компонент вектора 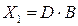нет отрицательных.

Исходя из этого, получаем следующие оценки нижних и верхних пределов устойчивости двойственных оценок при изменении каждого ограничения в отдельности.

Пределы уменьшения (нижняя граница) 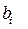определяются по тем 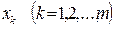, для которых соответствующие элементы обратной матрицы 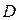больше нуля : .

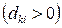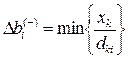Пределы увеличения (верхняя граница) 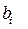определяются по тем 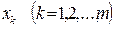, для которых соответствующие элементы обратной матрицы 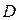меньше нуля : .

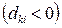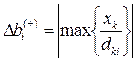Определим интервалы устойчивости двойственных оценок для примера 1.6.3.1:

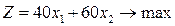
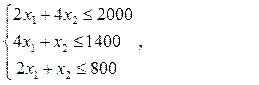
В матричной форме данная модель имеет вид:

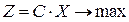
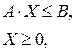
где 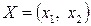- вектор переменных;

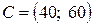- вектор коэффициентов при переменных в целевой функции;

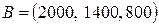- вектор свободных членов ограничений исходной задачи;

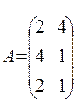- матрица коэффициентов системы ограничений.

После приведения системы ограничений к каноническому виду 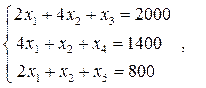матрица А примет вид: .

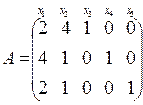С ненулевыми значениями в оптимальный план вошли переменные 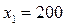, , 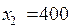, 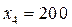следовательно, матрица 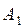будет составлена из первого, второго и четвертого столбцов матрицы 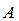: 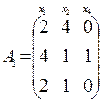. Для вычисления интервалов устойчивости двойственных оценок необходимо найти матрицу 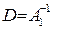, то есть 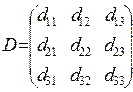(правила вычисления обратной матрицы были рассмотрены в курсе «Математика»,): .

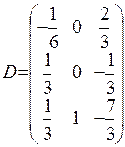Эту же матрицу 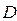можно получить и из последней симплексной таблицы 1.6.3.6, расположив в ней строки по возрастанию индексов базисных переменных и взяв коэффициенты при дополнительных переменных (таблица 1.6.3.8).

Таблица 1.6.3.8

Переменные прямой задачи	Основные	Дополнительные	Свободные члены,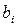
Базисные переменные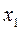
			-
					-
					-
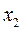
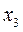
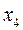
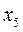
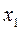
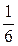
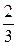
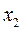
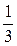
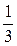
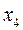
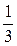
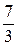
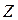
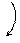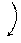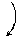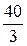
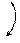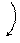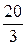
	0	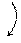0		0		32000
Переменные двойственной задачи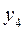
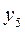
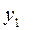
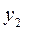
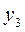
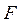
Дополнительные	Основные

В Таблице 1.6.3.8 три базисных переменных, следовательно, 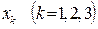, 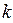- номер строки, то есть 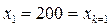, , 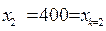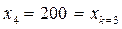. Найдем интервалы устойчивости первого ресурса 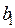(труд):

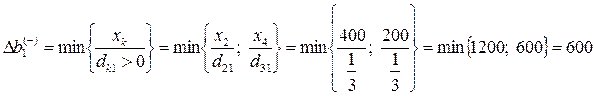, то есть ресурс «труд» можно уменьшать на 600 человеко-дней до величины 1400 человеко-дней 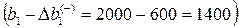, при этом двойственная оценка этого ресурса не изменится;

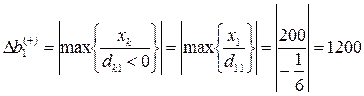, следовательно, ресурс «труд» можно увеличивать на 1200 человеко-дней до величины 3200 человеко-дней 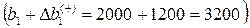и двойственная оценка этого ресурса также не изменится.

Таким образом, при изменении запасов ресурса «труд» 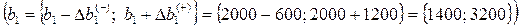в пределах от 1400 до 3200 человеко-часов двойственная оценка его не изменится.

Предположим, что запас ресурса «труд» увеличился на 30 человеко-дней, то есть теперь он составляет 2000 + 30 = 2030, человеко-дней. Определим, как изменится при этом прибыль.

Изменение ресурса «труд» находится в интервалах устойчивости двойственных оценок 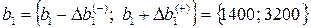, поэтому можно воспользоваться теоремой об оценках: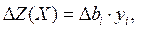 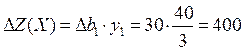. Значит, объем прибыли увеличится на 400 у.е., то есть 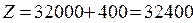у.е.

Такой же ответ мы получили бы, если бы решили симплексным методом задачу с новым ограничением по ресурсу «труд» (2030 человеко-дней).

Новый оптимальный план при увеличении запаса ресурса «труд» на 30 человеко-дней имеет вид:

, , , .

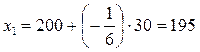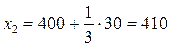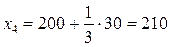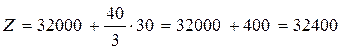Структурных сдвигов в полученном решении не произошло (то есть базисные переменные остались те же), но значения переменных изменились: продукции вида А будет выпущено на 5 единиц меньше, а продукции вида 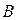- на 10 единиц больше. Значение целевой функции увеличится на 400 у.е.

Найдем интервалы устойчивости второго ресурса – «сырье». Этот ресурс в оптимальном решении используется не полностью и поэтому не имеет верхней границы интервалов устойчивости. Определим нижнюю границу:

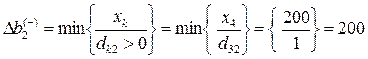, следовательно, .

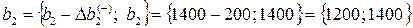Интервалы устойчивости третьего ресурса «оборудование»: ; ;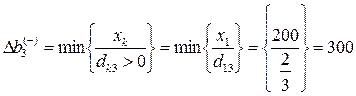

.

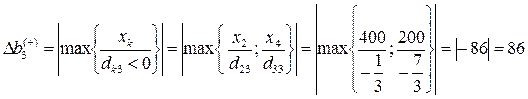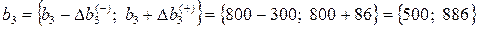Пусть запасы ресурсов изменяются одновременно, например, 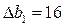(ресурс «труд» увеличим на 16 человеко-часов), 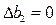(ресурс «сырье» в оптимальном плане используется не полностью, и поэтому нет смысла его увеличивать), 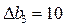(ресурс «оборудование» увеличим на 10 штук). Все изменения запасов ресурсов находятся в пределах устойчивости двойственных оценок, следовательно, решение двойственной задачи останется тем же: 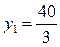, , 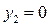, , 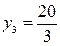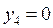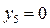. Так как ненулевым компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи, то положительным значениям переменных 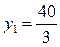, 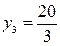оптимального решения двойственной задачи соответствуют нулевые значения переменных прямой задачи 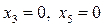(таблица соответствия 1.6.3.7). Поэтому остальные компоненты оптимального решения прямой задачи можно найти непосредственно из системы ограничений (1.6.3.2), подставив в нее 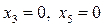и , , :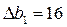

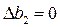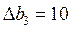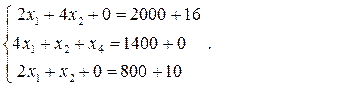
Решив эту систему, получим новое решение: 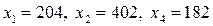. Значение целевой функции 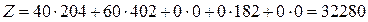, то естьпри увеличении ресурсов продукции вида 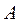будет производиться на 4 единицы больше, продукции вида 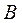будет производиться на 2 единицы больше, недоиспользование сырья уменьшится на 18 т (200 – 182 = 18) и прибыль получаемая от реализации всей продукции составит 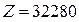у.е.