Соотвествия между множествами и их элементами
Если элементы 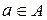 попарно сопоставляются с элементами
попарно сопоставляются с элементами 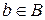 и способ сопаставления определен, то между множествами А и В установлено соответствие. Множество
и способ сопаставления определен, то между множествами А и В установлено соответствие. Множество 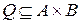 определяет закон, по которому установлено соответствие, и называется графиком соответствия. В соответствии, определяемом тройкой множеств (A, B, Q), кортежи
определяет закон, по которому установлено соответствие, и называется графиком соответствия. В соответствии, определяемом тройкой множеств (A, B, Q), кортежи  указывают пары сопоставляемых элементов.
указывают пары сопоставляемых элементов.
Пример 1.13. При выдаче студентам заданий на курсовое проектирование имеем: А – множество студентов, В – множество составленных заданий. График 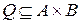 определяет, какое задание необходимо выполнить каждому студенту (установлено соответствие).
определяет, какое задание необходимо выполнить каждому студенту (установлено соответствие).
Пример 1.14. Ведомость с результатами сдачи экзамена группой студентов представляет график соответствия 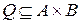 , где А – обозначает множество студентов группы, а В – множество оценок.
, где А – обозначает множество студентов группы, а В – множество оценок.
В общем случае соответствие может устанавливаться не для всех элементов А и В.
Множество А называется областью отправления соответствия, а множество В – областью прибытия. Проекцию 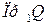 , состоящую из элементов
, состоящую из элементов 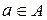 , называют областью определения соответствия, а проекцию
, называют областью определения соответствия, а проекцию 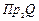 состоящую из элементов
состоящую из элементов 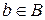 - областью значений соответствия. Если
- областью значений соответствия. Если 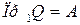 , то соответствие называют всюду определенным (в противном случае – частичным). В случае
, то соответствие называют всюду определенным (в противном случае – частичным). В случае  соответствие называют сюръективным.
соответствие называют сюръективным.
Всюду определенное соответствие (X, Y, Q), при котором область определения соответствия совпадает с областью отправления, называется отображением X в Y и обозначается
 (для
(для  ).
).
В общем случае элементу 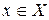 может ставиться в соответствие некоторое подмножество
может ставиться в соответствие некоторое подмножество 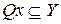 , называемое образом элемента x. Такое отображение называется многозначным. Так, например, англо-русский словарь дает многозначное отображение множества X включенных в него английских слов в множество Y русских слов. При однозначном отображении образом элемента
, называемое образом элемента x. Такое отображение называется многозначным. Так, например, англо-русский словарь дает многозначное отображение множества X включенных в него английских слов в множество Y русских слов. При однозначном отображении образом элемента 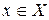 является один определенный элемент
является один определенный элемент 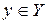 .
.
В случае однозначного отображения график соответствия, обозначаемый f, не имеет кортежей с одинаковыми первыми и различными вторыми компонентами. Такое отображение
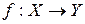
называют функцией. Элемент x из области определения 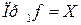 называют аргументом, а образ элемента x в области значений – значением функции. При этом соответствие (X, Y, f) записывают в виде
называют аргументом, а образ элемента x в области значений – значением функции. При этом соответствие (X, Y, f) записывают в виде
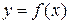 .
.
Если область отправления Х является конечным множеством, то функция может быть представлена конечным списком пар 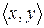 в виде таблицы. Функция может быть задана формулой, выражающей вычислительную процедуру, которая по любому заданному значению аргумента х выдает соответствующее значение у. Если X и Y является множествами вещественных чисел, то график функции
в виде таблицы. Функция может быть задана формулой, выражающей вычислительную процедуру, которая по любому заданному значению аргумента х выдает соответствующее значение у. Если X и Y является множествами вещественных чисел, то график функции 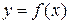 можно изобразить совокупностью точек на вещественной плоскости
можно изобразить совокупностью точек на вещественной плоскости 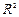 . Каждая точка соответствует определенному кортежу
. Каждая точка соответствует определенному кортежу 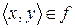 . Графическое представление множества f называется также графиком функции.
. Графическое представление множества f называется также графиком функции.
Областью отправления соответствия может быть упорядоченное множество Т моментов времени t. Тогда отображение f множества Т на множество вещественных чисел R
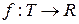 ,
,
будет состоять из пар  , где
, где 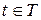 и
и  , называемых мгновенными значениями функции. Совокупность мгновенных значений
, называемых мгновенными значениями функции. Совокупность мгновенных значений  для всех
для всех 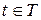 называется функцией времени
называется функцией времени 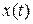 . Если t принимает любое значение в интервале
. Если t принимает любое значение в интервале 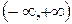 , то
, то 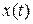 называют функцией с непрерывным временем.
называют функцией с непрерывным временем.
Иногда время можно рассматривать как бесконечное множество натуральных чисел 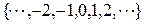 . Тогда
. Тогда 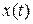 будет функцией с дискретным временем, и график соответствия ее будет представлять совокупность отсчетов
будет функцией с дискретным временем, и график соответствия ее будет представлять совокупность отсчетов 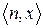 в моменты времени n.
в моменты времени n.
Частным случаем отображения является отображение множества самого в себя:
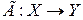 .
.
Отображение, заданные на одном множестве и определяемые парой 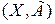 , называется отношениями. Множество Х является областью задания отношения, а график отношения имеет вид
, называется отношениями. Множество Х является областью задания отношения, а график отношения имеет вид
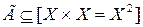 .
.
Поскольку каждое отдельно взятое отношение – упорядоченная пара – сопоставляет два элемента множества 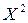 , такое отношение называют бинарным. Символически бинарные отношения между элементами x и y записывают в виде xГy.
, такое отношение называют бинарным. Символически бинарные отношения между элементами x и y записывают в виде xГy.
Отношения могут обладать следующими свойствами:
- рефлексивностью -  , [xГx];
, [xГx];
- симметричностью -  , [xГy→yГx];
, [xГy→yГx];
- транзитивностью - 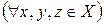 , [xГy, yГz→xГz];
, [xГy, yГz→xГz];
- тождественностью -  , [xГy,yГx→x=y].
, [xГy,yГx→x=y].
Бинарные отношения на конечном множестве могут быть записаны в виде матрицы размерностью 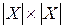 , строки и столбцы которой соответствуют элементам множества Х. При наличии между элементами отношения на пересечении соответствующих строк и столбцов ставят 1, при отсутствии – 0.
, строки и столбцы которой соответствуют элементам множества Х. При наличии между элементами отношения на пересечении соответствующих строк и столбцов ставят 1, при отсутствии – 0.
Пример 1.15. Для множества групп крови 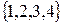 отношение совместимости при переливании определяется графиком
отношение совместимости при переливании определяется графиком
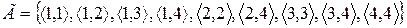 .
.
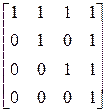
Матрица отношения имеет вид:
Пример 1.16. На множестве натуральных чисел 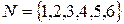 задано отношение xГy вида x имеет с y общий делитель отличный от единицы. Очевидно, что отношение между элементами будут обладать свойствами рефлексивности и симметричности. Матрицей отношений будет
задано отношение xГy вида x имеет с y общий делитель отличный от единицы. Очевидно, что отношение между элементами будут обладать свойствами рефлексивности и симметричности. Матрицей отношений будет
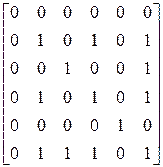 .
.
Отношение называется полным, если высказывание
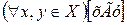
всегда истинно ( то есть  ), и пустым, если всегда ложно (
), и пустым, если всегда ложно ( 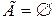 ). Полное отношение задается матрицей из одних единиц, а пустое – нулевой матрицей. Высказывание
). Полное отношение задается матрицей из одних единиц, а пустое – нулевой матрицей. Высказывание
 , [xГy→x=y],
, [xГy→x=y],
определяет отношение равенства. Если отношение рефлексивно, симметрично и транзитивно, то оно называется отношением эквивалентности.
Отношение неравенства могут определять порядок расположения элементов множества. Различают отношения нестрогого порядка  , обладающее свойствами:
, обладающее свойствами:
- рефлексивности - 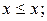
- тождественности - 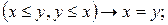
- транзитивности - 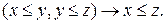
Отношение строгого порядка 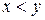 характеризуется свойствами:
характеризуется свойствами:
- антирефлексивности - x<x ложно;
- несимметричности - (x<y и y<x) ложно;
- транзитивности - (x<y и y<z)  x<z.
x<z.
Отметим, что на отношения переносятся операции над множествами – объединение, пересечения, разность.
Контрольные вопросы
1) Как вводится понятие функции при помощи множеств?
2) Как определяются области аргумента и значений функции?
3) Какое отображение называется отношением?
4) Как задаются бинарные отношения при помощи матриц?
5) Какие отношения называются эквивалентными?
Дата добавления: 2014-12-27; просмотров: 1779;
