Множества и подмножества

Если все элементы множества В содержатся в множестве А и, наоборот все элементы множества А содержатся в множестве В, то множества А и В называют совпадающими, или равными и обозначают А=В. Например, если А – множество треугольников с двумя равными сторонами, а В – множество треугольников с двумя равными углами, то А=В.

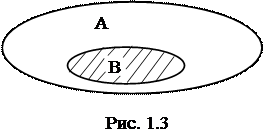
Если каждый элемент множества В является одновременно элементом множества А, причем В не совпадает с А, то множество В называется подмножеством множества А (Рис. 1.3). В этом случае множество В объединяет часть элементов множества А на основе как общих, так и частных признаков, которыми обладают не все элементы 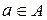. Такое соотношение между множествами называется включением и обознается символом :

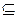- В содержится, включается в А,

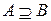- А содержит, включает В.

Пример 1.1. Если А – множество студентов группы, а В – множество отличников группы, то .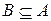

Пример 1.2. Если А – множество электроизмерительных приборов на складе, а В – множество амперметров среди них, то .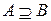

Символы 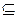и не исключают того, что множества В может оказаться совпадающим с множеством А. Если же множество В содержит не все элементы множества А, то соотношение между ними записывается с помощью символов строгого включения или 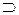. Так если А – множество пар перчаток, а В – множество правых перчаток, то 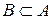и .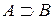

Используя логические символы импликация и 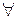квантор общности, определение подмножества можно записать в виде:

,

что означает: если В является подмножеством А, то для любого b (для всех b) утверждение b принадлежит В влечет за собой утверждение b принадлежит А.

Подмножества обладают следующими свойствами:

- рефлексивности - 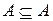, каждое множество является подмножеством самого себя;

- транзитивност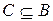и - и .

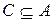Пустое множество является подмножеством любого множества, например возьмем произвольное множество М, то .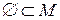

Если А и В – конечные множества, то при 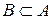мощность подмножества В меньше мощности множества А. Если же А бесконечное множество, то подмножество 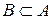может оказаться равномощным основному множеству А. Например, элементы множества (1.2) принадлежат и множеству (1.1), следовательно (1.2) является подмножеством (1.1) и в тоже время оба множества как эквивалентные равномощны.

Контрольные вопросы

1) Как вводится понятие множества?

2) Какие множества называются эквивалентными?

3) Как вводится понятие мощность множества?

4) Какие множества называются счетными, несчетными, упорядоченными и неупорядоченными?

5) Как вводится понятие подмножество заданного множества?