Введение в теорию множеств

Множеством называют совокупность объектов (элементов множества), объединенную на основе общего для них признака. Например, множество букв казахского алфавита состоит из 42 букв – элементов множества.

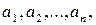Обычно множества обозначают прописными буквами латинского алфавита A,B,…,X,Y,Z, а их конкретные элементы – строчными буквами с индексами или без индексов Множество А, состоящее из элементов обозначаемое 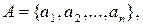изображают графически в виде некоторой замкнутой области, а его элементы – точками внутри этой области (Рис. 1.1). Принадлежность элемента множеству обозначается символом , например: 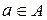- элемент а принадлежит множеству А; 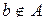- элемент b не является элементом множества А.

Самый простой способ задания множества – перечисление его элементов. Так, множество цифр десятичной системы можно записать в виде {0,1,2,3,4,5,6,7,8,9}. Но этот способ применим только к конечным множествам, для которых существует натуральное число N, определяющее общее число элементов множества. Бесконечное множество, содержащее бесконечное число элементов, определяется (задается) обычно свойствами его элементов: множество равносторонних треугольников, множество точек плоскости и т.п. Для краткой записи понятий и определений теории множеств используют ряд символов. Так, для описательного задания множества отрицательных чисел можно записать

.

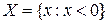Это означает: множество состоит из элементов x, обладающих тем свойством, что x – отрицательное число.

Другие логические символы будут поясняться по мере их появления.

Множество, не содержащее ни одного элемента, называется пустым и обозначается символом . Пустое множество является аналогом нуля (но не нулем) и условно относится к конечным множествам. Например множество отличников студенческой группы может оказаться пустым (S=0, отличников нет), но мы можем формально оперировать этим множеством.

Для сравнения множеств используют критерий мощность множества, строгого определения которого пока не существует. Понятие мощности множества связывают, прежде всего с числом элементов, но при сравнении бесконечных множеств это теряет смысл. Поэтому критерий мощность множества должен трактоваться несколько шире.

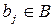Предположим, что между элементами множеств А и В можно установить взаимно однозначное соответствие, то есть каждому элементу поставить в соответствие один определенный элемент и, наоборот, с каждым сопоставить только один определенный элемент 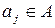. В этом случае множества называются эквивалентными, что обозначается А~В. Такие множества обладают следующими свойствами:

- рефлексивности – каждое множество эквивалентно самому себе, то есть А~А;

- симметрии – если множество А эквивалентно множеству В, то и множество В эквивалентно множеству А, то есть если А~В, то В~А;

- транзитивности (переходности) - если А~В, а В~С, то и А~С.

Рассмотрим несколько множеств: множество сторон квадрата, множество оценок знаний в ВУЗе (отлично, хорошо, удовлетворительно, неудовлетворительно), множество основных действий математики (сложение, вычитание, умножение, деление), множество сторон света (север, юг, восток, запад). Каждому элементу одного из множеств может быть сопоставлен один из элементов другого множества, то есть все множества попарно эквивалентны. И единственно общим у этих разнородных множеств будет число их элементов – четыре. Рассмотренные эквивалентные множества равномощны. Поэтому можно определить мощность произвольного множества как то общее, что имеется у всех множеств, эквивалентных данному.

Понятие мощность множества позволяет сравнивать бесконечные множества без подсчета числа их элементов. Возьмем два бесконечных множества: множество целых положительных чисел

{1,2,3,4,5,6,….}, (1.1)

и множество квадратов этих же чисел:

{1,4,9,16,25,36,….}. (1.2)

Взаимно однозначное соответствие между элементами обоих бесконечных множеств налицо. Поэтому множества (1.1) и (1.2) эквивалентны и равномощны.

Если все элементы бесконечного множества могут быть перечислены и занумерованы в виде бесконечной последовательности, например 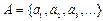, то такое множество называется счетным. Например, множество четных чисел, множество нечетных чисел, множество дробей вида 1/n и тому подобные множества. Бесконечное счетное множество равномощно множеству положительных целых чисел. В соответствии со свойствами транзитивности все бесконечные счетные множества эквивалентны между собой.

Бесконечные множества, элементы которых нельзя перечислить и пронумеровать, называются несчетными. Примером такого множества может служить линейное точечное множество. Простейшие разновидности линейных точечных множеств – отрезок и интервал.

Отрезком (сегментом) называют множество точек числовой оси, удовлетворяющих неравенству

.

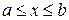Граничные точки x=a и x=b включены в отрезок. Отрезок обазначают символом [a,b].

Интервал (промежуток) – множество точек числовой оси удовлетворяющих неравенству

a<x<b.

Граничные точки в интервал, обозначенный (a,b), не входят.

Бесконечные несчетные множества содержат непрерывную последовательность элементов и имеют мощность континуума (от латинского слова continuum – непрерывный).

Множество называт упорядоченным, если любые два его элемента являются сравнимыми, что определяет какой-то порядок в размещении элементов. Примером упорядоченного множества может служить множество моментов времени Т. Его элементы t сравниваются на основе понятий раньше и позже. Свойство направленности времени выражается в том, что любой элемент 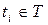предшествует элементу . Элементы упорядоченных множеств могут сравниваться на основе понятий меньше и больше. Пример – множество натуральных чисел.

Если множество представляется в виде последовательности элементов, причем каждому элементу этой последовательности отведено строго определенное место, то мы также имеем упорядоченное множество, называемое кортежем. Запись <a,b,c> означает, что кортеж состоит из трех элементов или компонент: а расположенном на первом месте, b на втором месте и с – на третьем месте. В отличие от неупорядоченных множеств, в кортеже могут иметься одинаковые компоненты, например <a,b,c,с>. Число компонент кортежа называют его размерностью, или длиной. В зависимости от длины n кортежи называют n-ками (двойками, тройками, четверками и так далее). Кортежи длиной два называют также упорядоченной парой. Кортеж, не содержащий ни одного элемента, называется пустым и обозначается .

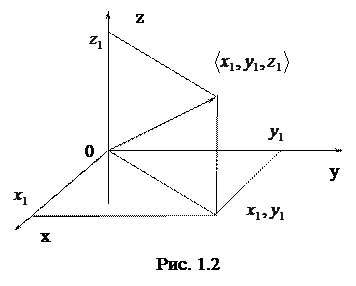Если компонентами кортежа являются вещественные числа, то его можно представить точкой в пространстве соответствующей размерности или вектором, проведенным из начала координат в точку, для которой компоненты вектора являются координатами. Так, кортеж 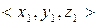представляют вектором в трехмерном пространстве (Рис. 1.2).

Проекции вектора на оси координат соответствуют его компонентам:

.

Проекции вектора на две оси

,

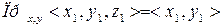Представляют собой проекцию вектора на плоскость 0ХУ.