Элементарные логические функции

Поскольку каждая логическая переменная может принимать только два значения, то при числе переменных n полное число возможных наборов конечно и равно m = 2 ⁿ.

Пример 3.2 При числе переменных n + 2 получим число наборов m = 2² = 4.

Множеством наборов будет 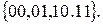Множество всех наборов задает область определения логический функции.

Каждому набору может соответствовать одно из двух значений логической функции – 0 или 1. Поэтому максимально возможное число различных функций от n аргументов также конечно и равно

N =2^m = 2²ⁿ,

При n=2 число различных функций N =2^{2 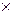2}= 16. В таблице 3.1. приведены все возможные функции двух переменных f(x,y), их значения для разных наборов (х,у) и их формулы.

Если разделить таблицу 3.1 по линии между функциям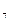и f и f , то функции в каждой части оказываются инверсными по отношению к симметричным им функциям из другой части. Например, 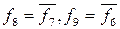и т.д. Помимо этого, из таблицы видно что все функции можно еще разбить на несколько разновидностей.

Значения функци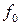й и 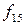не зависят от значений переменных, т.е. переменные и х является фиктивными аргументами. Число таких функций, называемых функциями-константами, определяется отсутствием действительных аргументов (n=0) и равно

Функция f₀ называется нулевой, соответствующий ей логический элемент – генератор нуля – показан на рисунке 3.4а. Функция f₁₅ называется единичной, ей соответствует логический элемент – генератор единиц (рисунок 3.4б).

У функции одна из переменных оказывается фиктивным аргументом. Фактически это функция одной переменной (n=1), и число их 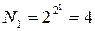. Но разновидностей функций одной переменной, существенно зависящих от своего аргумента, всего две, функции называется повторением, тавтологией, а соответствующий логический элемент – повторитель (рисунок 3.4в). Функции f₁₀ f₁₂ являются рассмотренными ранее функциями инверсии.

Таблица 3.1

X					Функция
Y

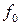
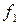
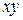
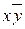
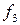
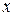
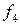
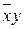
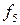
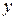
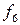
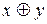
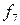
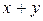
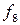
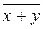
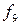
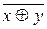
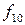
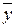
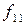
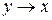
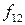
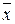
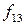
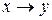
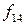
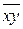
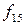
Функции 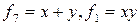являются также рассмотреннымранее дизъюнкцией и конъюнкцией. С помощью функции инверсии 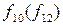дизъюнкции f₇ и конъюнкции f₁ может быть выражена любая другая логическая функция.

Функция 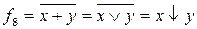называется функцией ИЛИ–НЕ, а также функцией Пирса, или стрелкой Пирса. Для нее справедливы соотношения:

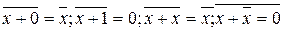
Логический элемент показан на рисунке 3.5а и называется ИЛИ- НЕ, элемент Пирса.

Функция 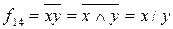называется функцией И–НЕ, функцией Шеффера, или штрихом Шеффера. Имеет место соотношения:

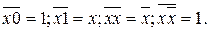
Логический элемент И-НЕ, элемент Шеффера приведен на рисунке 3.5б.

Функция 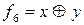обозначает сложение по модулю 2. Через основные логические операции может быть выражена в виде

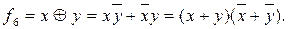
Как видно из таблицы 3.1, f₆=1 только при противоположных значениях переменных. Поэтому ее называют также неравнозначностью. Справедливы соотношения:

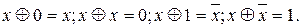
Стандартный логический элемент сложение по модулю 2 приведен на рисунке 3.6а. Функция

,

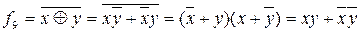принимает значение 1 только при одинаковых значениях х и у. Поэтому ее называют функцией равнозначности или эквивалентности и обозначают также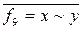

Справедливы соотношения ; ; ; .

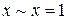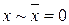Функции f₉ соответствуют два стандартных логических элемента: сложение по модулю 2 с отрицанием (рисунок 3.6 б) и эквивалентность (рисунок 3.6в).

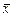Функция f₁₃ =x y (читается «если х, то у») называется импликацией. Как видно из таблицы 3.1, f₁₃=1, если х=0 или у=1, и f₁₃=0 только при х=1 и у=0. Поэтому она может быть представлена в виде: f₁₃= х y= +у.

Стандартный логический элемент - импликация (рисунок 3.7а).

Инверсная импликации функция

.

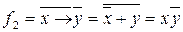Называется запретом, т.к. при у =1 ее значение равно 0 при любых значениях х.

Логический элемент запрет показан на рисунке 3.7б.

Функция 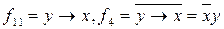отличается от функций 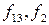лишь порядком размещения входных переменных и не являются оригинальным.

Рассмотренные функции одной и двух переменных называются элементарными логическими функциями. С их помощью, используя принцип суперпозиции (возможно, многократно) можно построить все логические функции от любого числа переменных.

Принцип суперпозиции заключается в функции, например:

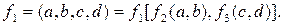
Набор логических функций (операций) считается полным набором, если он позволяет представить любую логическую функцию. Таким набором является совокупность функций инверсии, конъюнкции и дизъюнкции. Полный набор может состоять и из одной функции, если он позволяет получить три основные логические функции. Примером может служить функция И-НЕ (штрих Шеффера).

Действительно,

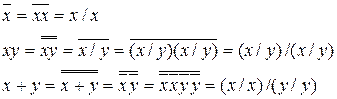
Другим примером полного набора является функция ИЛИ-НЕ (стрелка Пирса), с помощью которой также можно представить

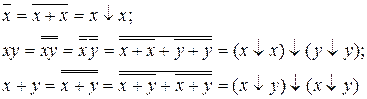
Следовательно полный набор из функций НЕ, И и ИЛИ обладает некоторой избыточностью. Но он применяется особенно часто, т.к. проще всего позволяет перейти от словесного выражения к логической функции. Вместе с тем, элементы И-НЕ и ИЛИ-НЕ являются базовыми элементами серий интегральных микросхем.

Поэтому при проектировании логических устройств приходится переводить логические выражения в базис ИЛИ-НЕ или И-НЕ. При этом используют, как было показано выше, законы де Моргана и свойство двойного отрицания.

Пример 3.3 Представить функцию

.

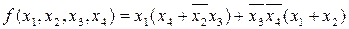в базисе И-НЕ. Заменив выражения в скобках по закону де Моргана и применив двойную инверсию, получим:

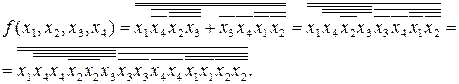
Контрольные вопросы

1) Как формируются элементарные логические функции двух переменных?

2) Назовите основные логические функции и соответствующие им логические элементы?

3) Какие логические функции образуют полные наборы?