Законы и тождества алгебры логики

В алгебре логики действует законы, называемые системой равносильных преобразований (равносильностями). Равносильность двух выражений подтверждается совпадением соответствующих таблиц истинности для всех наборов переменных или совпадением множеств истинности.

Приведем основные законы и тождества алгебры логики.

1) П ер е м е с т и т е л ь н ы й (коммутативный) закон:

ху = ух; х + у = у + х.

2) Со ч е та т е л ь н ы й (ассоциативный) закон:

xyz=x(yz)=(xy)z;

x+y+z=x+(y+z)=(x+y)+z.

3) Р а с п р е д е л и т е л ь н ы й ( дистрибутивный) закон:

конъюнкции относительно дизъюнкции –

x(y+z)=xy+xz;

дизъюнкции относительно конъюнкции –

x+yz=(x+y)(x+z).

4) Законы ин в е р с и и (законы де Моргана):

а) инверсия конъюнкций есть дизъюнкция инверсий-

б) инверсия дизъюнкций есть конъюнкция инверсий –

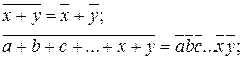
в) обобщение законов де Моргана, предложенное Шенноном -

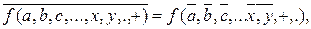
т.е. инверсия любой функции получается заменой каждой переменной на инверсную с одновременной взаимной заменой символов конъюнкции.

5. формула (двойную инверсию можно снять).

6) При конъюнкции 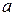и некоторой функции соответствующие переменные в функции заменяются на 1, а инверсные – на 0, а при дизъюнкции – наоборот:

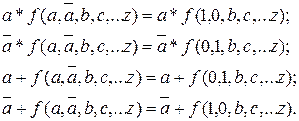
Из этих тождеств вытекает следующие равносильности, называемые законом поглощения:

a+ab=a; a+ab+ac+…+az=a;

a(a+b)=a; a(a+b)(a+c)…(a+z)=a.

7) Законы склеивания:

а) полного склеивания

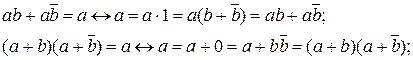
б) неполного склеивания

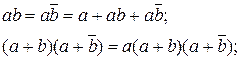
в) обобщенного склеивания

8)

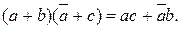
Использование рассмотренных законов и тождеств позволяет упрощать сложные логические функции путем равносильных преобразований.

Пример 3.1Преобразование логической функции:

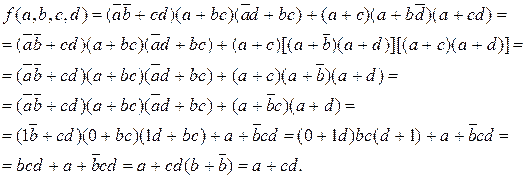
Таким образом, логическая переменная оказалась в исходной функции фиктивной (значение функции от нее не зависит).

В логических преобразованиях установлен следующий порядок выполнения операций:

1) инверсия;

2) конъюнкция;

3) дизъюнкция;

4) другие операции, соответствующие логическим функциям, которые будут рассмотрены ниже.

Скобки в логических выражениях проставляется для выделения отдельных сочетаний или для изменения установленного порядка преобразований.

Контрольные вопросы

1) Дайте определение логической функции, логической переменной

2) Как выполняется операция инверсии?

3) Как выполняется операция логического умножения или конъюнкция?

4) Как выполняется операция логического сложения или дизъюнкция?

5) Дайте определение основных законов алгебры логики?