Введение в теорию матриц

Прямоугольной матрицей называется упорядоченная совокупность вещественных или комплексных чисел, расположенных в виде прямоугольной таблицы, содержащей n строк и m столбцов

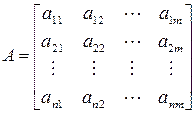
В этом определении важно подчеркнуть, что матрица - это не просто таблица. При определенном заданном расположении ее элементов она является математическим объектом и понимается как единое целое, так как установлены определенные математические операции над ее элементами (сложение, умножение и другие действия).

Элементы матрицы всегда имеют двойной индекс а_ij (i- строка, j-столбец). Если число строк n равно числу столбцов, матрица является квадратной. Число n опре­деляет порядок матрицы. Матрица, содержащая n строк и m столбцов, имеет размерность (n×m). Квадратная матрица имеет размерность (n×m).

Элементы, имеющие одинаковые индексы, a₁₁, a₂₂,…, a_nn, расположены на главной диагонали.

Матрица, состоящая из одной строки, называется строкой или вектор-строкой; матрица, состоящая из одного столбца - столбцом или вектор-столбцом. Вектор-строка имеет размерность 1×m; вектор-столбец - n×1.

Матрица называется диагональной, если на главной диагонали стоят элементы, отличные от нуля:

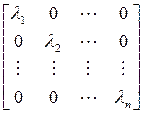
Диагональная матрица, у которой все числа, расположенные на главной диагонали, равны между собой, называется скалярной.

Матрица называется единичной, если все числа, стоящие на главной диагонали, равны 1.

Матрица называется треугольной, если все ее элементы под главной диагональю или над ней равны нулю. Верхняя и нижняя треугольные формы имеет вид соответственно:

, .

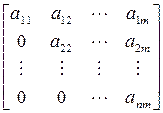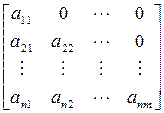Матрица, все элементы которой равны нулю, называется нулевой и обозначается через 0.

Матрицы равны друг другу, если имеют одну и ту же размерность и их соответствующие элементы равны между собой.

Если повернуть матрицу вокруг главной диагонали, это приведет к тому, что строки и столбцы поменяются местами. Эта операция «зеркального» отражения называется транспонированием и обозначается А^т. При транспонировании неквадратных матриц их следует преобразовать в квадратные.

При транспонировании имеют место свойства:

; ; ; .

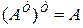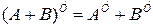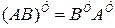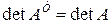Если матрица не меняет своего значения при транспони­ровании 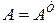, она симметрична относительно главной диагонали и называется симметрической.

Произведение 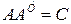представляет собой симметрическую матрицу, так как

.

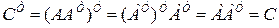Если .матрица А при транспонировании меняет знак

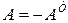
она называется кососимметрической. У кососимметрической матрицы главная диагональ состоит из нулевых элементов.

Матрица А* называется эрмитовой, если она получается транспонированием и элементы ее комплексно сопряжены к элементам матрицы А:

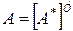
Заметим, что симметрическая матрица с вещественными элементами является эрмитовой. Матрица А, для которой

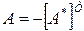
называется косоэрмитовой. Симметрическими и эрмитовыми матрицами могут быть только квадратные матрицы.

С понятием матрицы тесно связано понятие определителя. Разница состоит в том, что матрица - это упорядоченная система чисел, над которыми можно выполнять математические операции, а ее определитель - это одно число, которое находится по известным правилам. Определитель обозначается det А или |А|.

Любой определитель, строки и столбцы которого «укладываются» в строки и столбцы матрицы, называется минором этой матрицы. Например, минор порядка k матрицы А есть определитель k-го порядка, составленный из элементов, находящихся на пересечении некоторых k строк и k столбцов матрицы А в их естественном расположении.

Рангом матрицы А называется максимальный порядок отличных от нуля миноров матрицы. Ранг отражает макси­мальное, число линейно независимых строк или столбцов матрицы.

Если матрица имеет определитель, равный нулю, она называется особенной или вырожденной.

Всякая неособенная квадратная матрица А имеет свою обратную А^-1. Матрица является обратной, если

,

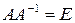где Е - единичная матрица.

Обратная матрица является единственной для заданной матрицы. Из этого следует, что 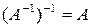. Очевидно также, что .

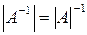Матрица называется ортогональной, если 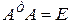. Ортогональная матрица всегда неособенная, так как А=±1.

Для ортогональной матрицы имеют место соотношения:

; .

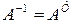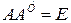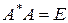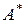Матрица А называется унитарной, если , где - транспонированная комплексно-сопряженная матрица Унитарная матрица всегда неособенная. Для нее справедливы соотношения 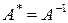, 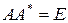. Заметим что вещественная ортогональная матрица унитарна.

Обратная матрица может быть получена, если каждый элемент транспонированной матрицы алгебраических дополнений разделить на свой определитель Δ:

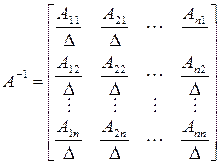
Вычисление алгебраических дополнений при высоких порядках связано с большим объемом вычислений и нецелесообразно даже при постановке задачи на ЦВМ. При решении задач на цифровых вычислительных машинах применяются иные способы обращения, излагаемые в специальных курсах по вычислительной математике.

Существуют, однако, классы матриц, которые легко обращаются. К такому классу, например, относятся диагональные матрицы.

Когда матрицы складываются, вычитаются или умножаются на скаляр они подчиняются обычным законам элементарной алгебры. Исключение составляет перемножение матриц, которое осуществляется по специальным правилам линейных алгебраических преобразований.