Характеристическое уравнение. Собственные числа и собственные векторы

Уравнение вида

,

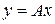может рассматриваться как порождение нового вектора у путем умножения матрицы А на вектор х. Если полученный таким образом вектор у совпадает в векторном пространстве по направлению с первоначальным вектором х, то составляющие вектора должны быть пропорциональны составляю­щим вектора х, т. е.

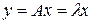. (4.5)

Число 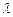в этом случае является коэффициентом пропорциональности.

Запишем систему (5) в развернутой форме

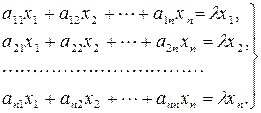. (4.6)

Перейдем к однородной системе, объединяя члены, расположенные в правой и левой частях уравнения (4.6):

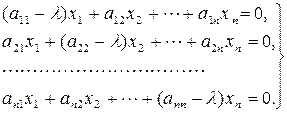. (4.7)

В матричном виде

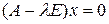. (4.8)

Матрица 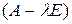отличается от А тем, что по диагонали вычитается число .

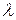Система (4.7) имеет нетривиальное, или ненулевое, решение (т. е. такое решение, в котором хотя бы одно из чисел x_i, отличается от нуля) лишь при условии, что определитель равен нулю, а именно

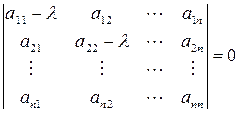. (4.9)

Перепишем уравнение (4.9) сокращенно в матричном виде

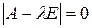. (4.10)

Определитель 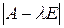называется характеристическим.

Разворачивая определитель 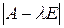по известным правилам, получим полином n-й степени относительно числа А. Приравнивая его к нулю, получим характеристическое уравнение

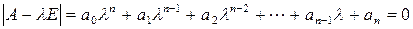. (4.11)

Корни характеристического уравнения (4.11) называются собственными или характеристическими числами матрицы. Совокупность всех собственных чисел называется спектром матрицы А.