Собственные векторы

Уравнение (4.5) имеет своим решением ненулевой вектор 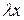только в том случае, если множитель пропорциональности 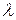равен хотя бы одному из собственных чисел матрицы А.

Каждая матрица размерности 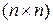всегда имеет ровно n собственных чисел. Некоторые из этих собственных чисел могут быть кратными (совпадающими). Для каждого возможного значения 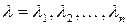может быть найдено решение однородной системы (4.8). Подставляя значение 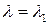в уравнение (4.8), получим вектор решения

.

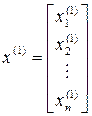Если подставить 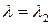получим второй вектор решения

,

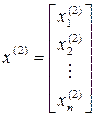и так далее, вплоть до . Последний вектор решения имеет вид

.

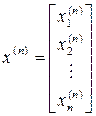Полученные 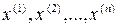векторов называются собственными векторами матрицы А. Таким образом, каждое собственное число порождает свой собственный вектор. Если собственные числа вещественной матрицы комплексны, координаты собственного вектора также будут комплексны.

Так как собственные векторы являются решениями однородной системы, то каждое решение определено лишь с точностью до произвольного ненулевого множителя, т. е. умножив решение на скалярный множитель, опять получим решение.

При умножении собственного вектора на любое произвольное, не равное нулю число изменяется лишь его длина, но направление в пространстве остается тем же. Таким образом, собственные векторы, образующие систему n решений в n мерном пространстве, однозначно определены лишь по направлению, но их длины (модули) могут быть произвольны.

Если собственные числа матрицы различны, то собственные векторы, порождаемые ими, линейно независимы. Система линейно независимых векторов образует базис пространства Rⁿ.

Примером базиса является совокупность векторов

,

,

...............................

.

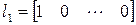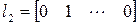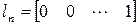Любой вектор 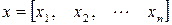может быть представлен в базисе из собственных векторов. В частности,

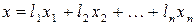
Число векторов, образующих базис, совпадает с размерностью пространства.

Если имеются кратные собственные числа, то вопрос о существовании линейно независимых векторов остается открытым. Им могут соответствовать линейно независимые собственные векторы, но могут и не соответствовать.

Отметим некоторые свойства симметрических матриц.

1) Собственные числа симметрической матрицы вещественны. Это относится также к тому случаю, когда элементы матрицы комплексно-сопряженные.

2) Собственные векторы симметрической матрицы ортогональны. Это значит, что их скалярное произведение равно нулю.

Если симметрическая матрица А имеет n различных собственных чисел 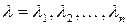то соответствующие собственные векторы 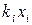образуют в n-мерном пространстве ортогональный базис.

Пример 4.4. Рассмотрим матрицу

Ее характеристическое уравнение имеет вид

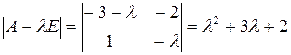
Собственные числа матрицы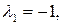

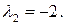
Найдем собственный вектор, порождаемый :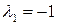

.

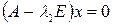
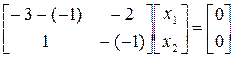
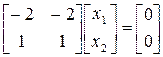Одно из решений уравнения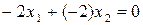

, .

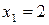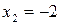Следовательно, собственный вектор, соответствующий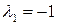

.

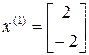Однако он не единственный. Решению уравнения 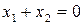удовлетворяет 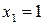, 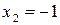. Поэтому собственный вектор

,

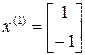также способствует собственному числу .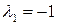

Найдем собственный вектор, порождаемый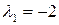

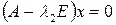
Для решения уравнения положим 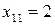, 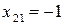. Собственный вектор, соответствующий 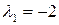, будет

.

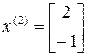Убедимся, что вектор 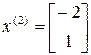также удовлетворяет 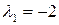. Эти векторы линейно независимы, следовательно, образуют базис пространства.

Пример 4.5 Рассмотрим симметрическую матрицу

, , , .

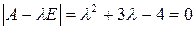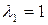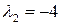Собственные векторы

, .

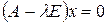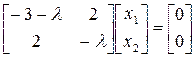При , , .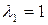

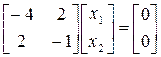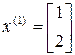При , , .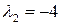

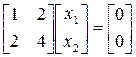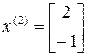Собственные векторы образуют ортогональный базис. Действительно, их скалярное произведение равно нулю:

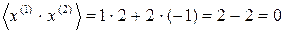
Контрольные вопросы

1) Какая матрица называется треугольной?

2) Приведите примеры треугольных матриц?

3) Как определяется характеристическое уравнение матрицы?

4) Как определяются собственные вектора матрицы?