Преобразование подобия

Говорят, что матрица В подобна матрице А, если они связаны соотношением

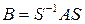, (4.20)

где S —неособенная матрица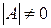

Соотношение (4.20) носит название преобразования подобия. Из него следует, что

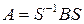
Преобразование подобия обладает следующими свойствами:

1) Преобразование суммы равно сумме преобразований

.

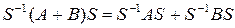2) Преобразование произведения равно произведению преобразований сомножителей

.

3. Преобразование обратной матрицы равно обратной матрице от преобразованной

.

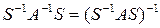4) Преобразование целой степени (положительной или отрицательной) равно той же степени преобразования

.

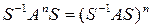Покажем, что подобные матрицы имеют одинаковые характеристические полиномы. Действительно,

.

Из этого свойства следует, что подобные матрицы имеют одинаковые собственные числа (в том числе кратные) и одинаковые следы. Можно показать, что свойство вектора быть собственным не зависит от выбора базиса. Поэтому собственные векторы подобных матриц связаны соотношением

,

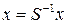где S — матрица преобразования координат.

Действительно, если

,

то

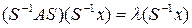
Если матрица ортогональна и, следовательно, 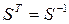, то имеет место ортогональное преобразование

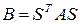
Контрольные вопросы

1) Раскройте смысл теоремы Кели-Гамильтона?

2) Как доказывается на примерах, то что матрица является решением своего характеристического уравнения?

3) Как определяется на основе теоремы Кели-Гамильтона обратная матрица?

4) Какие матрицы называются подобными?