Матричные степенные ряды
Пусть имеется последовательность матриц Ak (k= 1, 2,...) размерности (h×h). Под пределом последовательности матриц Ak .понимается матрица

Если предел последовательности матриц существует, то матричный ряд является сходящимся. Если предела не существует, матричный ряд расходится.
Пользуясь понятием предела матрицы, можно ввести в рассмотрение матричный степенной ряд
 . (4.22)
. (4.22)
Ряд (4.22) сходится, если все собственные числа  матрицы А расположены в замкнутом круге радиуса
матрицы А расположены в замкнутом круге радиуса  скалярного степенного ряда:
скалярного степенного ряда:
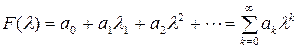 ,
, 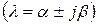 , (4.23)
, (4.23)
причем собственные числа, лежащие на окружности, являются простыми.
Матричный степенной ряд расходится, если хотя бы одно собственное число матрицы А находится вне круга сходимости скалярного степенного ряда (4.23) или имеется собственное число матрицы А, лежащее на окружности круга сходимости, для которого ряд (4.23) расходится.
Таким образом, для того чтобы матричный степенной ряд (4.22) сходился к некоторой матрице, необходимо и достаточно, чтобы скалярный ряд (4.23) сходился на спектре матрицы А. Так как степенной ряд можно по частям дифференцировать любое число раз внутри круга сходимости, то ряд (4.22) сходится на спектре любой матрицы, собственные числа которой попадают внутрь круга сходимости. Следовательно, разложение функции 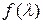 в степенной ряд в круге
в степенной ряд в круге 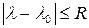 сохраняет силу, если скалярный элемент
сохраняет силу, если скалярный элемент  заменить любой матрицей А, все собственные числа которой лежат внутри круга сходимости радиуса R.
заменить любой матрицей А, все собственные числа которой лежат внутри круга сходимости радиуса R.
Подробный анализ сходимости матричных степенных рядов приводится в более полных руководствах. Укажем некоторые наиболее важные тождества, связывающие функции от скалярного аргумента с матричными значениями аргумента.
Из тождества
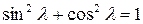 ,
,
для любой матрицы А следует
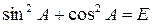
Точно так же для любой матрицы А
 , тогда
, тогда 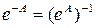 .
.
Далее, для любой матрицы А
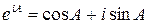 .
.
Экспоненциальная функция может быть представлена в виде:
 ,
,
 .
.
Этот ряд сходится равномерно и абсолютно. Умножение скалярных величин 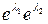 коомутативно, однако соответствующее произведение экспоненциальных матриц нельзя представить в виде
коомутативно, однако соответствующее произведение экспоненциальных матриц нельзя представить в виде 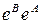 , если матрицы А и В не коммутируют.
, если матрицы А и В не коммутируют.
Тригонометрические функции имеют вид:
 ,
,
 ,
,
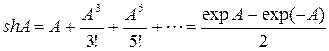 ,
,
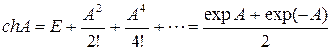 ,
,
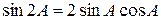 .
.
Дата добавления: 2014-12-27; просмотров: 3737;
