Линейная динамическая система

Понятие линейной динамической системы на уровне физических представлений обычно опирается на так называемый принцип суперпозиции, заключающийся в том, что общий выходной эффект от совокупности входных воз- действий на систему может быть получен суммированием выходных величин от каждого воздействия в отдельности. Существует даже мнемоническая формула суперпозиции: «Следствие от суммы причин является суммой следствий от каждой из причин в отдельности». Однако с точки зрения общих определений, сформулированных в предыдущих параграфах, нам нет необходимости прибегать к столь неточным и туманным, с точки зрения математики, исходным данным. Сформулируем понятие линейной динамической системы, опираясь на определения 5.1 и 5.2.

Определение 5.6. Линейной динамической системой называется математическая модель совокупности взаимосвязанных элементов, удовлетворяющая аксиомам определения 5.1 и следующим условиям:

1) Заданы линейные (векторные) пространства состояний системы Х, мгновенных входных воздействий U, их допустимых значений Ω, мгновенных значений выходных величин У и их допустимых значений Г.

2) Переходная функция состояния 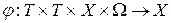созначениями

,

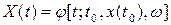является линейной на множестве 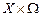, то есть имеет место соотношение

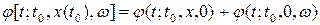, (5.21)

и удовлетворяет дифференциальному уравнению

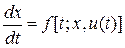. (5.22)

3) Выходное отображение 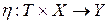линейно на множестве Х, то есть справедливо соотношение

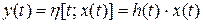. (5.23)

Мы дали определение обыкновенной линейной динамической системе, то есть системы, движение которой описывается дифференциальными уравнениями. Конкретизируем это общее определение, используя свойства линейного пространства.

Пусть в линейном пространстве Х определен базис и установлена размерность пространства n. Пусть, далее, пространство входных сигналов Ω имеет размерность 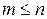. Состояние системы в данный момент времени t будет определяться вектором Х в пространстве состояний. Тогда производная этого вектора 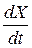, также являющаяся вектором, может быть разложена по координатам базиса на n составляющих 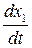, ,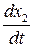…, 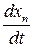. В силу условия 2 определения 5.6 правая часть уравнения (5.22) линейна на множестве 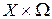, то есть она является линейной комбинацией векторов X и U. Следовательно, составляющие вектора 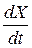можно представить в виде

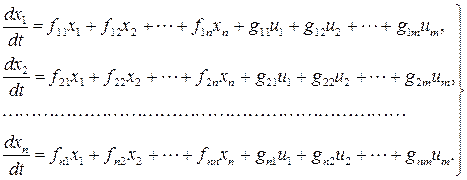, (5.24)

где функции 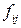, 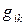являются координатами векторов X и U.

Введем запись векторов в виде матриц-столбцов

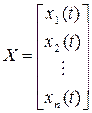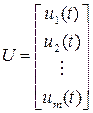, . (5.25)

и запись координатных функций в виде матриц

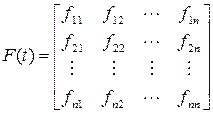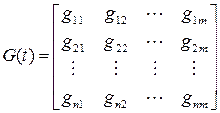, . (5.26)

Матрица F (t) имеет n строк и n столбцов, матрица G(t) имеет n строк и т столбцов. Используя правило умножения матриц, уравнения (5.24) можно записать в виде

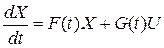. (5.27)

Пусть пространство выходных величин F имеет размерность р. Тогда, в силу условия 3 определения 5.6, формула (5.23) может быть представлена в виде линейной комбинации составляющих вектора Х и проекций вектора Y:

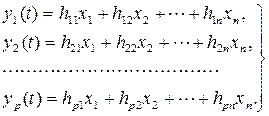(5.28)

Записывая вектор Yв виде матрицы-столбца

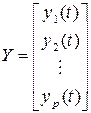, (5.29)

и вводя матрицу координатных функций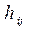

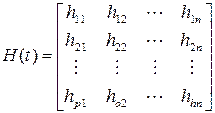, (5.30)

получим соотношения (5.28) в виде

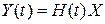. (5.31)

Определение 5.7. Линейная динамическая система (конечномерная и с непрерывным временем) описывается следующей системой линейных дифференциальных уравнений:

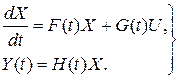. (5.32)

Если матрицы F, G и Н не зависят от времени, линейная динамическая система будет стационарной.

Первое уравнение (5.28) называется уравнением состояний системы, второе - уравнением выходных величин.