Динамическая система

Обычно, когда что-либо называют системой, то имеют в виду совокупность взаимосвязанных элементов или частей, взаимодействующих с окружающей средой по определенным закономерностям. Более конкретно, система – это устройство, комплекс, объединение, характерное наличием входов, то есть некоторых физических величин или явлений, характеризующих результат воздействия внешней среды на движение самого устройства, комплекса, объединения. В этом, довольно общем описании понятия системы специально не предусматривается конкретизация физических параметров системы, поскольку мы хотим сформулировать строгое определение понятия системы в самом общем виде, пригодном для широкого класса задач.

Для изучения процессов, протекающих в системах, необходимо уметь определять по текущим значениям входных воздействий выходные величины системы. Для этого необходимо, очевидно, тем или иным образом описать саму систему на языке математики, или, как принято говорить, создать математическую модель системы. В теоретическом плане описание ситсемы предполагает лишь знание ее состояния в данный и последующий моменты времени. Это состояние должно полностью опредеяться математическими соотношениями, однозначно установленными для данной системы.

Таким образом, изложенные физические и логические представления приводят нас к общей схеме системы, показанной на рисунке 5.1.

Рассмотрим теперь входные воздействия, состояние системы и выходные величины подробнее, с целью получения более точных формулировок.

Входные воздействия естественно в общем случае можно отнести к некоторому определенному множеству их мгновенных значений, которое обозначим через U, и к множеству моментов времени, которое обозначим через Т. Это будет означать, что конкретное входное воздействие принадлежит в данный момент времени t множеству U. Очевидные физические соображения требуют, чтобы множество моментов времени Т было упорядоченным, иными словами, в нем должно быть определено направление времени. Очевидно, это направление должно быть выбрано так, чтобы прошлое предшествовало будущему.

В общем случае нельзя считать, что входное воздействие является любой произвольной функцией времени. Обычно необходимо в каждом конкретном случае вводить определенные ограничения. Они диктуются, главным образом, условиями решаемой задачи, свойствами воздействующей окружающей среды и тому подобное, но всегда должны иметь место. Если обозначить абстрактное правило построения допустимых функций через ω, то множество Ω допустимых значений функций можно определить следующим образом:

.

Напомним, что это выражение читается так: на множествах T и U задано соответствие (правило) ω, такое, что множество T отображается в множество U, образуя множество отображений Ω. Очевидно, Ω есть подмножество множества T´U. Для конкретноых значений величин прведенных выше выражение можно было бы записать так:

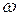= (t).

В дальнейшем, применяя запись , мы всегда будем подразумевать, что эта функция принадлежит допустимому множеству.

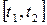Поскольку в реальных системах мы имеем дело только с отрезками входных воздействий (так протяженность времени всегда ограничена), класс функций на множестве Ω должен быть таким, чтобы две различные функции и на соседних отрезках времени и 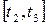могли быть заменены одной функцией 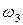на суммарном отрезке (Рисунок 5.2).

Это условие запишем следующим образом. Пусть

тогда должно иметь место условие:

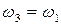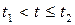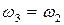при ,

при .

Описание входных воздействий приведенных выше выражениями оказывается вполне достаточным для их использования в дальнейшем.

Рассмотрим теперь понятие состояние системы. Пока, не имея более строгих формулировок, можно говорить о состоянии системы как о таких данных о ее настоящем и прошлом, которые необходимы для определения текущего и будущего значений выходных величин системы. Говоря более конкретно, мы должны предположить, что существуют некоторые величины (обозначим их через х), характеризующие состояние системы в данный момент времени, которые зависят от предыдущего состояния, текущего времени и входных воздействий. Запишем эту закономерность в общем виде так:

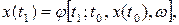
где - данный момент времени; - некоторый предшествующий момент времени 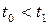; 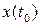- состояние системы предшествующее данному; 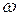- входное воздействие, причем .

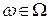Если рассамтривать величины х как элементы некоторого множества Х, а все моменты времени ( в том числе и ) принадлежащими множеству Т, то формулу для состояний х можно записать в более общей форме:

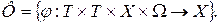
Множество содержит в качестве своих элементов упорядоченные четверки в виде , , , , 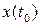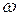следовательно соответствие (правило ) 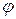устанавливает отображение (функциональную связь) этих четверок на множестве Х, содержащиее элементы х. Полученное отображение принадлежит некоторому множеству Ф и имеет специальное наименование – переходная функция системы.

Переходная функция состояния должна удовлетворять ряду требований, определяющих однозначность введенного определения.

Во-первых, естественно потребовать, чтобы переходная функция состояния была определена для всех , а при 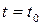имело место равенство:

,

для всех , и 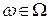. Это равенство определяет согласованность функции 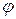с ее начальным значением и независимость начального значения 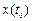от данного значения входного сигнала 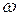(Рисунок 5.3). Далее, знание состояния системы 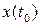в момент 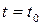и отрезка входного воздействия 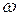на отрезке времени (обозначим ) должно быть необходимым и достаточным условием, позволяющим определить состояние системы в момент 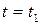. Поэтому должно иметь место соотношение

.

Система, удовлетворяющая этому соотношению, называется динамической.

При этом два одинаковых входных воздействия на заданном отрезке времени и при заданном начальном состоянии системы 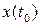должны давать один и тот же результат, иными словами, должно выполняться равенство:

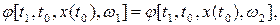
если при .

Наконец, одно и тоже входное воздействие 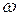должно определять состояние системы на конце заданного промежутка времени независмимо от того, действовало ли оно отдельно на промежутках времени или сразу на всем промежутке (Рисунок 5.4). Это условие определяется равенством

,

для всех , и 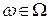и любых .

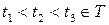Свойства переходной функции состояния системы, устанавливаемые рассмотренными соотношениями, полностью определяют ее как основную характеристику системы.

Выходные величины системы могут быть определены, если заданы входные воздействия и известна переходная функция состояния системы. Поскольку последняя уже включает в себя эффект входного воздействия, выходная величина (обозначим ее y(t)) может быть представлена в виде

.

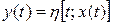Обычно на множестве выходных величин не накладывается особых ограничений, однако в случае необходимости они должны принадлежать некоторому множеству Г. Поскольку моменты времени t принадлежат множеству T, а значения х – множеству Х, множество выходных величин можно представить в более общей форме так:

.

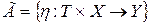Теперь приведем полную формулировку определения динамической системы, принадлежащую Р. Калману, П. Фалбу и М. Арбибу.

Определение 5.1.Динамической системой называется математическая модель совокупности взаимосвязанных элементов, удовлетворяющая следующим аксиомам:

1) Заданы множество моментов времени Т, множество состояний системы Х, множество мгновенных значений входных воздействий U, множество их допустимых значений:

множество мгновенных значений выходных величин Y и множество их допустимых значений

.

2) Множество Т есть некоторое упорядоченное подножество множества вещественных чисел (направление времени): .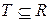

3) Множество входных воздействий удовлетворяет условиям:

а) множество 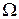непусто;

б) отрезок входного воздействия 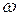на промежутке времени 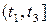обладает следующим свойством (свойство сочленения):

если 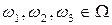и

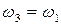то при 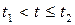, (5.1)

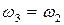при .

4) Существует переходная функция состояния

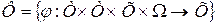, (5.2)

значениями, которой являются состояния системы

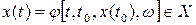, (5.3)

в котором она оказывается в момент , если в начальный момент времени t₀, она была в начальном состоянии и если на нее действовало входное воздействие .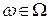

Переходная функция состояния обладает следующими свойствами:

а) функция определена для всех и не обязательно для всех (направление времени);

б) функция согласована со своим начальным значением, то есть равенство

, (5.4)

выполняется для любых ;

в) для всех отрезков входных воздействий , таких, что 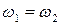для всех , имеет место равенство:

. (5.5)

г) функция обладает полугрупповым свойством, то есть для любых 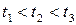, 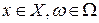имеет место равенство:

. (5.6)

5) Задано выходное отображение:

(5.7)

определяющее, значения выходных величин системы

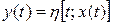. (5.8)

Приведенное определение в наиболее общем виде описывает математическую модель динамической системы. Схематически ее можно представить в виде структурной схемы изображенной на рисунке 5.5. Эта метематическая модель применима к различным классам физических систем, что с теоретической точки зрения весьма важно, так как при этом большое количество частных приложений объединяется общей терминологией, основными понятиями и фундаменталоьными результатами теории.

Отдельные дополнительные термины конкретизируют математическую модель динамической системы. Так, состояние системы х в момент t₀, или пара элементов множества Т×Х, называется событием или фазаой системы. Само множество Т×Х называется пространством событий или фазавым пространством.

В том случае, когда некоторое множество входных воздействий используется для управления системой, оно называется управлением. Управление переводит (или преобразует) состояние системы х(t₀) в состояние . При этом система находитсяв движении, описывая в пространстве траекторию.

Динамическая система называется свободной или автономной, если множество допустимых входных воздействий 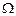содержит только один элемент. Практически это означает, что входные воздействия отсутствуют и система совершает движение лишь из-за наличия начальных отклонений.

Важным классом динамических систем являются системы, переходная функция состояния которых удовлетворяет дифференциальному уравнению. Построим определение такой системы на основе общего определение 5.1.

Введем метрики на множествах моментов времени Т, входных воздействий 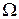и состояний системы Х. Тогда перечисленные множества будут метрическими пространствами, Примем в качестве элементов этих пространств действительные числа R. При этом получим: 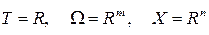, где m и n размерности пространств, а сами пространства будут нормированными или векторными.

Потребуем, чтобы переходная функция состояния 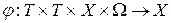была непрерывным отображением в любой точке 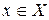для каждого .

Если теперь состояние системы в момент времени t определяется соответствующим значением переходной функции состояния

То приращение x при бесконечно малом изменении t в силу непрерывности функции j может быть записано следующим образом:

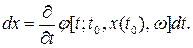
Положим, далее, что функция 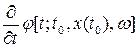однозначно соответствует некоторая непрерывная функция . Тогда состояние системы определяется следующим дифференциальным уравнением:

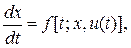
где 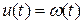. Назовем систему, удовлетворяющую перечисленным выше условиям: обыкновенной динамической системой и дадим полное ее определение.

Определение 5.2. Обыкновенной динамической системой называется математическая модель совокупности взаимосвязанных элементов, удовлетворяющая аксиомам определение 5.1, у которой:

1) Множество моментов времени T есть числовая ось вещественных чисел, а множества мгновенных значений входных воздействий U, допустимых значений входных воздействий Ω и состояний системы Х есть векторные просранства.

2) Функция 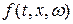, называемая производящей и задаваемая функцией 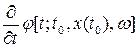, непрерывна для каждого значения .

3) Переходная функция состояния системы является решением дифференциального уравнения:

, (5.9)

с начальными условиями 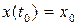для всех , и , где x – вектор состояния системы, u– вектор входных воздействий.

В ряде случаев в динамической системе имеют место условия, при которых физические элементы и их взаимосвязи не меняются с течением времени. При этом состояние системы, определяемое переходной функцией состояния, не зависит от начала отсчета времени.

Если например, задано входное воздействие из класса воздействий 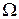и система имеет значение переходной функции состояния 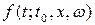, то сдвиг по времени на величину этого воздействия повлечет за собой сдвиг на такую же величину переходной функции состояния без изменения ее формы (Рисунок 5.6).

Более точно такие системы определяются следующим образом.

Определение 5.3. Динамическая система называется стационарной (или с независимыми от времени параметрами), если выполняются следующие условия:

1) Пространство допустимых входных воздействий 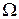содержит все функции для любых t, .

2) Справедливо равенство

, (5.10)

для всех .

3) Отображение 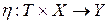, определяющее выходные величины 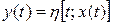, не зависит от t, то есть выполняется равенство:

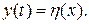(5.11)

Динамическая система будет системой с непрерывным временем, когда Т есть множество всех вещественных чисел. Когда Т есть множество целых чисел, система будет с дискретным временем.

Контрольные вопросы

1) Дайте определение понятия системы?

2) Как определяются входные и выходные воздействия системы?

3) Как определяется состояние системы?

4) Как определяется динамическая система?