Норма матрицы

Нормирование векторов и .матриц широко применяется в вычислительной математике для оценки быстроты сходимости числовых последовательностей и рядов.

Под нормой матрицы А понимается действительное число , удовлетворяющее условиям:

1) , причем 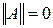тогда и только тогда, когда ;

2) 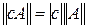(с - число) и, в частности, |;

3) ;

4) .

Норма матрицы может быть введена многочисленными способами. Отметим три наиболее распространенных способа задания нормы:

1) ;

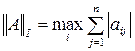2) ;

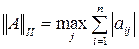3) .

Пример 4.9 Вычислим нормы матрицы

;

;

.

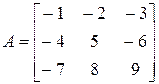
Контрольные вопросы

1) Зачем производится диагонализация матриц?

2) Как составляется каноническая форма Жордана?

3) Как определяется функция от матрицы?

4) Как записываются основные функции от матриц?

5) Как на основе соотношений Сильвестра формируется функция от матрицы?

6) Как вычисляется норма матрицы?