Теорема Сильвестра
Соотношение Сильвестра представляет собой способ эффективного выражения функций от матрицы, если только эта функция может выражаться в виде матричного полинома.
Пусть матрица А имеет n различных собственных чисел. Тогда для произвольного матричного полинома 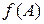 справедливо разложение
справедливо разложение
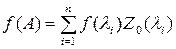 ,
,
где
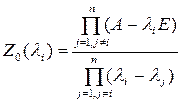
В качестве примера вычислим функцию 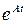 для матрицы
для матрицы
 ,
,  ,
, 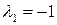 ,
, 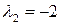 .
.
Функция 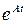 может быть представлена в виде сходящегося степенного ряда. Следовательно, теорема Сильвестра может быть применена. Соотношение Сильвестра позволяет непосредственно получить
может быть представлена в виде сходящегося степенного ряда. Следовательно, теорема Сильвестра может быть применена. Соотношение Сильвестра позволяет непосредственно получить 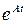 вместо того, чтобы суммировать бесконечный ряд по степеням матрицы А.
вместо того, чтобы суммировать бесконечный ряд по степеням матрицы А.
В силу соотношения Сильвестра для данной матрицы имеем:
 ,
,  ,
,  .
.
Вычислим матрицы  и
и 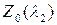 , соответствующие собственным числам
, соответствующие собственным числам 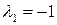 ,
, 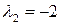
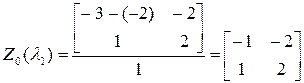 ,
, 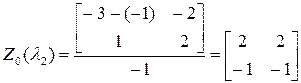 .
.
Функция от матрицы 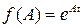 определяется следующим образом:
определяется следующим образом:
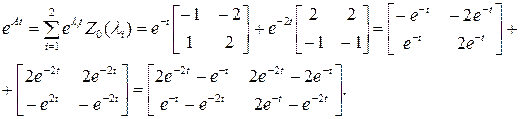
Дата добавления: 2014-12-27; просмотров: 1833;
