Функции от матриц

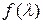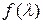Пусть задана функция скалярного аргумента и некоторая квадратная матрица А. Требуется распространить функцию на матричные значения аргумента. Теорема Кели- Гамильтона дает решение этой задачи, если 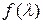- полином. Тогда матричная функция 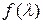является суммой с такими же коэффициентами, как у полинома, при соответствующих степенях матрицы А. Исходя из свойств теоремы Кели - Гамильтона, функция 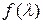определяется и в более общем случае. В случае полиномов некоммутативный характер матриц не играет роли. Каждая матрица коммутирует сама с собой и со своей произвольной степенью.

Будем считать, что функция 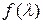определена на спектре матрицы А, если под подразумевать собственные числа матрицы А. Тогда все функции 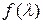, имеющие одни и те же значения на спектре матрицы А, должны иметь одно и то же матричное значение 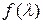. Значения функции 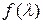, определенные на спектре матрицы А, полностью определяют 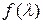. Функция 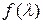называется функцией от матрицы.

Имеет место следующее важное свойство, основанное па преобразовании подобия. Если матрицы А и В подобны и матрица S преобразует А в В:

,

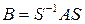то 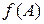и 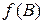также подобны, и матрица S преобразует 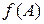в :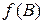

.

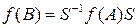Доказательство этого результата вытекает из того свойства, что подобные матрицы имеют одинаковые характеристические (и минимальные) полиномы и, следовательно, функция 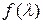принимает одни и те же значения как на спектре матрицы А, так и на спектре матрицы В.