Связь между собственными числами и элементами матрицы. След матрицы
Рассмотрим две простые закономерности, связывающие собственные числа и элементы матрицы А. Они вытекают из известной теоремы Виета. Положив в уравнении (4.11) 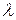 = 0, получим
= 0, получим
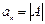 . (4.12)
. (4.12)
Следовательно, свободный член характеристического уравнения равен определителю матрицы А.
Запишем характеристический полином в виде произведения сомножителей, полагая все собственные числа 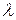 i различными:
i различными:
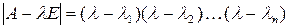 . (4.13)
. (4.13)
При 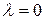 получим
получим
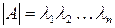 .
.
Следовательно, определитель матрицы А равен произведению всех собственных чисел 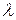 i. Из этого свойства следует, что если хотя бы одно из
i. Из этого свойства следует, что если хотя бы одно из 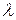 i равно нулю, матрица А - особенная.
i равно нулю, матрица А - особенная.
Уравнение в форме (4.13) дает возможность выразить коэффициенты при различных степенях л через собственные числа. Например, коэффициент при 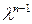 равен
равен
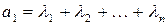 . (4.14)
. (4.14)
С другой стороны, раскрывая определитель 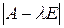 , найдем, что коэффициент при
, найдем, что коэффициент при 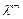 равен сумме диагональных элементов:
равен сумме диагональных элементов:
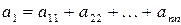 . (4.15)
. (4.15)
Таким образом, сумма диагональных, элементов матрицы равна сумме ее собственных чисел.
Ввиду важности этих свойств сумме диагональных элементов присвоено особое название - след матрицы. След матрицы А обозначается Sp А или tr А. Таким образом,
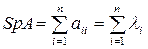 . (4.16)
. (4.16)
Справедливы следующие соотношения:
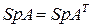 ,
, 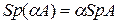 ,
, 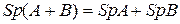 ,
, 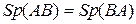 .
.
Дата добавления: 2014-12-27; просмотров: 5854;
