Метод Даламбера решения задачи Коши для уравнения свободных колебаний струны
Как мы видим, общие решения дифференциальных уравнений с частными производными зависят уже не от произвольных постоянных, а от произвольных функций. Определяя соответствующим образом эти функции, можно удовлетворять тем или иным дополнительным условиям. Этот факт проиллюстрируем на примере задачи Коши для уравнения колебаний струны.
Итак, рассмотрим следующую задачу Коши:найти функцию 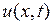 , непрерывную при
, непрерывную при 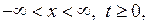 так чтобы она удовлетворяла уравнению (4.2) при
так чтобы она удовлетворяла уравнению (4.2) при 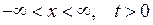 и начальным условиям
и начальным условиям
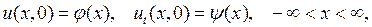 (5.1)
(5.1)
где 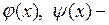 заданные функции.
заданные функции.
Предположим, что решение 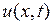 задачи Коши существует. Так как функция
задачи Коши существует. Так как функция 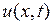 удовлетворяет уравнению (4.2), то она необходимо должна иметь вид (4.9). Произвольные функции
удовлетворяет уравнению (4.2), то она необходимо должна иметь вид (4.9). Произвольные функции 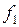 и
и 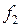 в (4.9) найдем так, чтобы функция (4.9) удовлетворяла начальным условиям (5.1). Подставляя (4.9) в (5.1), получаем
в (4.9) найдем так, чтобы функция (4.9) удовлетворяла начальным условиям (5.1). Подставляя (4.9) в (5.1), получаем
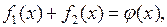
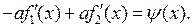 (5.2)
(5.2)
Интегрируя второе равенство в (5.2), имеем
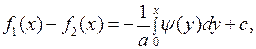 (5.3)
(5.3)
где 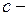 произвольная постоянная интегрирования.
произвольная постоянная интегрирования.
Решая первое уравнение в (5.2) вместе с (5.3), для функций 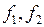 получаем выражения вида
получаем выражения вида
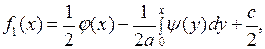
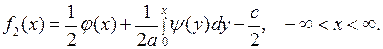 (5.4)
(5.4)
Если теперь (5.4) подставить в (4.9), то будем иметь:
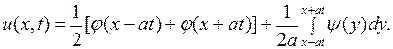 (5.5)
(5.5)
Формула (5.5) называется формулой Даламбера.
При выводе формулы (5.5) мы предполагали существование решения задачи Коши. Предположим, что функция 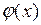 дважды, а функция
дважды, а функция 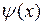 один раз непрерывно дифференцируемы при
один раз непрерывно дифференцируемы при 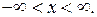 Тогда непосредственной подстановкой (5.5) в уравнение (4.2) и в начальные условия (5.1) можно убедиться, что функция (5.5) действительно является единственным решением задачи Коши.
Тогда непосредственной подстановкой (5.5) в уравнение (4.2) и в начальные условия (5.1) можно убедиться, что функция (5.5) действительно является единственным решением задачи Коши.
Пример. Найти решение 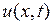 уравнения
уравнения 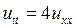 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 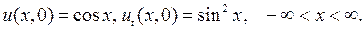
Решение.Так как 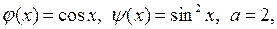 то внося эти значения в формулу Даламбера (5.5), получаем
то внося эти значения в формулу Даламбера (5.5), получаем
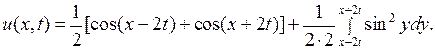
Вычислим интеграл
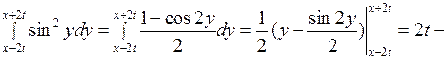
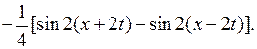
Так как 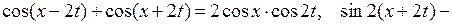
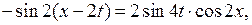 то решение задачи Коши окончательно можно записать в виде
то решение задачи Коши окончательно можно записать в виде
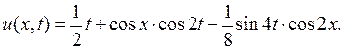
Задачи
Используя формулу Даламбера, найти решения 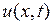 следующих задач Коши (-
следующих задач Коши (- 
5.1. 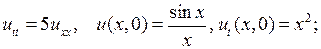
5.2.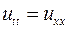 ,
, 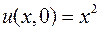 ,
, 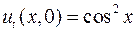 ;
;
5.3.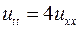 ,
, 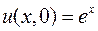 ,
, 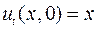 ;
;
5.4.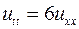 ,
, 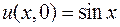 ,
, 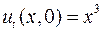 ;
;
5.5.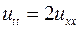 ,
, 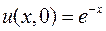 ,
, 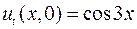 ;
;
5.6.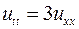 ,
, 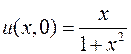 ,
, 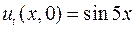 ;
;
5.7.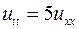 ,
, 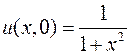 ,
, 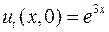 ;
;
5.8.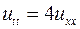 ,
, 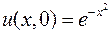 ,
, 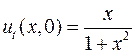 .
.
Дата добавления: 2017-03-29; просмотров: 6725;
