Нахождение общих решений некоторых дифференциальных уравнений с частными производными
Как известно, общее решение обыкновенного дифференциального уравнения 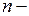 го порядка представляется функцией от независимой переменной
го порядка представляется функцией от независимой переменной 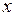 и
и 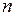 произвольных постоянных интегрирования
произвольных постоянных интегрирования 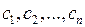 :
:
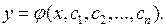 (4.1)
(4.1)
Зная это общее решение, можно решить ту или иную задачу, например, задачу Коши, определяя соответствующим образом постоянные 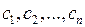 .
.
Для дифференциальных уравнений с частными производными невозможно указать единого вида общего решения, аналогичного (4.1), но можно находить его в отдельных частных случаях путем непосредственного интегрирования их канонических форм. Этот факт мы проиллюстрируем на некоторых примерах уравнений.
Пример 4.1. Найти общее решение уравнения колебаний струны
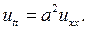 (4.2)
(4.2)
Решение. Сначала приведем его к каноническому виду. Характеристическое уравнение (3.9) в нашем случае имеет вид:
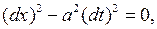
а его общие решения -
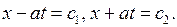
Следовательно, в соответствии с (3.12) за новые переменные 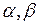 берем
берем
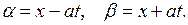 (4.3)
(4.3)
Так как
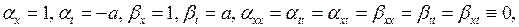
то из формул (3.4) получим
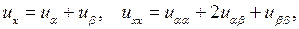
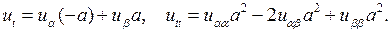
Подставив эти значения 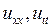 в уравнение (4.2), получим канонический вид уравнения колебаний струны
в уравнение (4.2), получим канонический вид уравнения колебаний струны
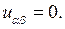 (4.4)
(4.4)
Найдем общее решение уравнения (4.4). Обозначим
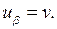 (4.5)
(4.5)
Тогда уравнение (4.4) примет вид
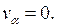 (4.6)
(4.6)
Уравнению (4.6) удовлетворяет любая функция, не зависящая от 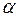 . Следовательно,
. Следовательно,
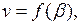 (4.7)
(4.7)
где 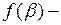 произвольная функция переменной
произвольная функция переменной 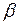 . Подставляя (4.7) в (4.5), имеем
. Подставляя (4.7) в (4.5), имеем
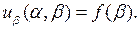 (4.8)
(4.8)
Проинтегрируем уравнение (4.8) по переменной 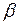 , рассматривая
, рассматривая 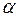 как параметр и беря постоянную интегрирования в виде произвольной функции этого параметра. В результате получим
как параметр и беря постоянную интегрирования в виде произвольной функции этого параметра. В результате получим
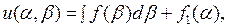
где 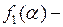 произвольная функция
произвольная функция 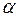 . Обозначив
. Обозначив 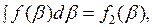 окончательно получим
окончательно получим
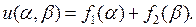
Возвращаясь к старым переменным 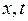 с помощью соотношений (4.3), будем иметь
с помощью соотношений (4.3), будем иметь
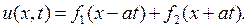 (4.9)
(4.9)
Нетрудно проверить, что функция (4.9) есть решение уравнения (4.2), если 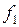 и
и 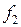 - произвольные дважды непрерывно дифференцируемые функции.
- произвольные дважды непрерывно дифференцируемые функции.
Выражение (4.9) является общим решением уравнения свободных колебаний струны (4.2).
Пример 4.2.Найти общее решение уравнения
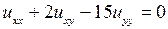 .
.
Решение. Сначала приведем его к каноническому виду. Составим ха-
рактеристическое уравнение и решаем его:
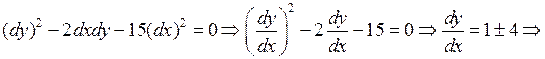
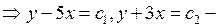 характеристики уравнения.
характеристики уравнения.
Следовательно, в соответствии с (3.12) за новые переменные 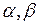 берем
берем
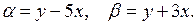
Так как
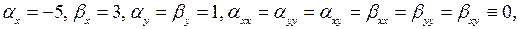
то из формул (3.4) получим
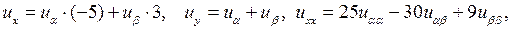
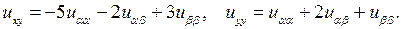
Подставим эти значения 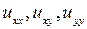 в уравнение:
в уравнение:
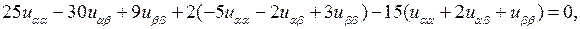
откуда получим его канонический вид: 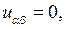 общее решение которого дается формулой (см. пример 4.1)
общее решение которого дается формулой (см. пример 4.1) 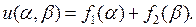 Возвращаясь
Возвращаясь
к старым переменным 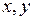 , получаем окончательно
, получаем окончательно
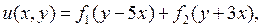
где 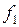 и
и 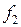 - произвольные дважды непрерывно дифференцируемые функции.
- произвольные дважды непрерывно дифференцируемые функции.
Пример 4.3.Найти общее решение уравнения
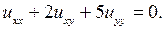
Решение. Составим характеристическое уравнение и решаем его:
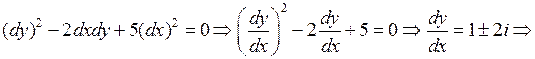
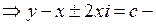 комплексно сопряженные характеристики уравнения.
комплексно сопряженные характеристики уравнения.
Поэтому за новые переменные 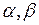 берем
берем
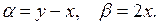
Так как
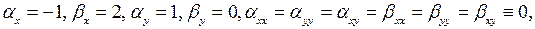
то из формул (3.4) получим
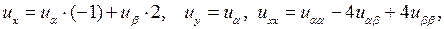
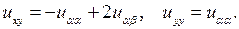
Подставим эти значения 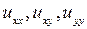 в уравнение:
в уравнение:
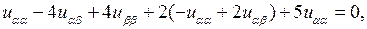
откуда получим его канонический вид: 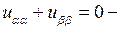 уравнение Лапласа.
уравнение Лапласа.
Из теории аналитических функций комплексного переменного известно, что действительная и мнимая части аналитической функции удовлетворяют уравнению Лапласа. Следовательно, общее решение уравнения Лапласа можно записать в виде
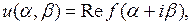
где 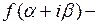 произвольная аналитическая функция аргумента
произвольная аналитическая функция аргумента 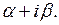 Возвращаясь к старым переменным
Возвращаясь к старым переменным 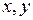 , получаем общее решение исходного уравнения в виде
, получаем общее решение исходного уравнения в виде
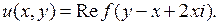
Пример 4.4.Найти общее решение уравнения
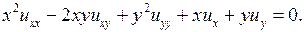
Решение. Составим характеристическое уравнение и решаем его:
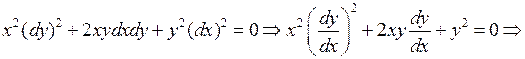
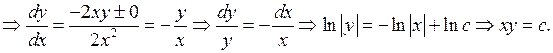
Итак, характеристическое уравнение имеет одно семейство действительных характеристик. Положим 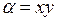 , а за
, а за 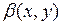 в соответствии с вышесказанным возьмем любую дважды непрерывно дифференцируемую функцию, для которой якобиан
в соответствии с вышесказанным возьмем любую дважды непрерывно дифференцируемую функцию, для которой якобиан 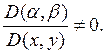 Например, пусть
Например, пусть 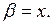 Тогда
Тогда
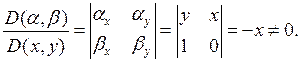
Так как
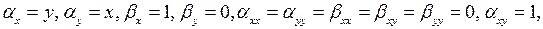
то подставляя эти значения производных в (3.4), получаем
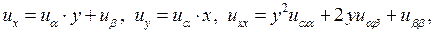
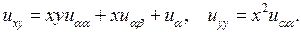
Теперь эти выражения производных внесем в исходное уравнение:
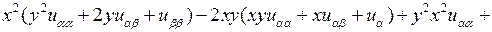
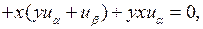
откуда 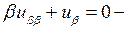 канонический вид уравнения. Решаем его. Обозначим
канонический вид уравнения. Решаем его. Обозначим 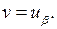 Тогда уравнение примет вид:
Тогда уравнение примет вид: 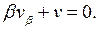 Это есть уравнение с разделяющимися переменными, при этом переменная
Это есть уравнение с разделяющимися переменными, при этом переменная 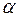 считается параметром. Получаем
считается параметром. Получаем
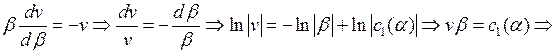
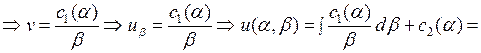
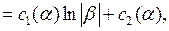
где 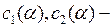 постоянные интегрирования, представляющие собой произвольные функции переменной
постоянные интегрирования, представляющие собой произвольные функции переменной 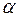 . Возвращаясь к старым переменным
. Возвращаясь к старым переменным 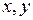 , получаем общее решение исходного уравнения в виде
, получаем общее решение исходного уравнения в виде
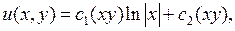
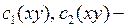 произвольные дважды непрерывно дифференцируемые функции аргумента
произвольные дважды непрерывно дифференцируемые функции аргумента 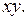
Задачи
Найти общее решение уравнений:
4.1. 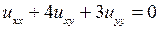 ; 4.2.
; 4.2. 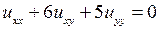 ;
;
4.3. 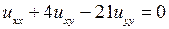 ; 4.4.
; 4.4. 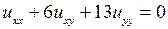 ;
;
4.5. 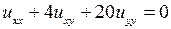 ; 4.6.
; 4.6.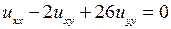 ;
;
4.7. 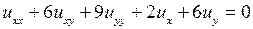 ;
;
4.8. 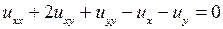 ;
;
4.9. 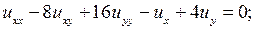
4.10. 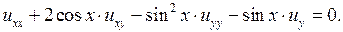
Ответы:
4.1. 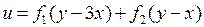 ; 4.2.
; 4.2. 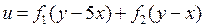 ;
;
4.3. 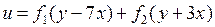 ; 4.4.
; 4.4. 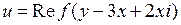 ;
;
4.5. 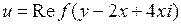 ; 4.6.
; 4.6. 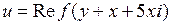 ;
;
4.7. 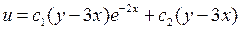 ; 4.8.
; 4.8. 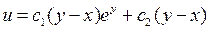 ;
;
4.9. 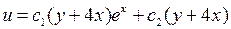 ;
;
4.10.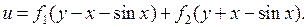
Дата добавления: 2017-03-29; просмотров: 1721;
