Метод Фурье решения начально- краевых задач для уравнения теплопроводности в тонком стержне
В настоящем параграфе метод Фурье применим к решению первой начально-краевой задачи для уравнения (2.31) теплопроводности в тонком стержне.
7.1. Случай однородного уравнения.Рассмотрим задачу:найти функцию 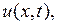 непрерывную при
непрерывную при 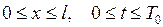 , удовлетворяющую уравнению
, удовлетворяющую уравнению
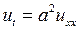 ,
, 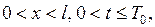 (7.1)
(7.1)
граничным условиям
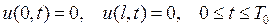 (7.2)
(7.2)
и начальному условию
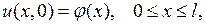 (7.3)
(7.3)
где 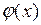 - заданная функция, имеющая непрерывную производную и
- заданная функция, имеющая непрерывную производную и 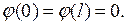
Ищем решение уравнения (7.1), удовлетворяющее условиям (7.2), в виде
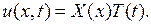 (7.4)
(7.4)
Подставляя (7.4) в уравнение (7.1) и разделяя переменные, получаем
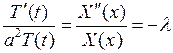
или
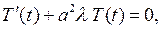 (7.5)
(7.5)
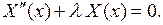 (7.6)
(7.6)
Кроме того, из граничных условий (7.2) следует, что
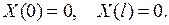 (7.7)
(7.7)
Итак, для определения функции 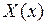 имеем задачу Штурма- Лиувилля (7.6), (7.7). Эта задача изучена нами в пункте 6.1 §6. Ее решение имеет вид:
имеем задачу Штурма- Лиувилля (7.6), (7.7). Эта задача изучена нами в пункте 6.1 §6. Ее решение имеет вид:
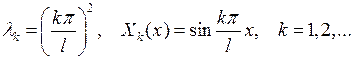 (7.8)
(7.8)
Подставляя значения 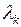 из (7.8) в уравнение (7.5), получаем
из (7.8) в уравнение (7.5), получаем
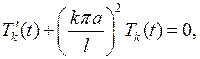
которое представляет собой дифференциальное уравнение с разделяющимися переменными. Его общее решение дается формулой
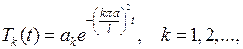 (7.9)
(7.9)
где 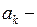 произвольные постоянные.
произвольные постоянные.
Теперь, если (7.8), (7.9) подставить в (7.4), то получим частные решения уравнения (7.1), удовлетворяющие граничным условиям (7.2), следующего вида
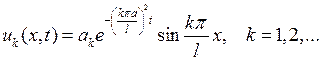
Чтобы удовлетворить начальному условию (7.3), составим ряд из этих частных решений:
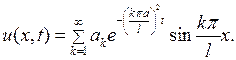 (7.10)
(7.10)
Подставляя (7.10) в условие (7.3), будем иметь:
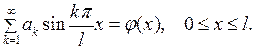 (7.11)
(7.11)
(7.11) есть разложение функции 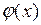 в ряд Фурье по синусам. Поступая как и в §6, приходим к тому, что соотношение (7.11) будет удовлетворено, если коэффициенты разложения (7.11) определены по формулам
в ряд Фурье по синусам. Поступая как и в §6, приходим к тому, что соотношение (7.11) будет удовлетворено, если коэффициенты разложения (7.11) определены по формулам
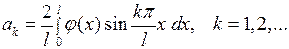 (7.12)
(7.12)
Подставляя (7.12) в (7.10), получаем решение задачи (7.1)- (7.3).
По поводу обоснования полученного решения в виде (7.10) необходимо сказать то же самое, что и в §6: ряд (7.10) и ряды, получаемые формальным почленным дифференцированием этого ряда дважды по 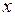 , один раз по
, один раз по 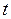 , сходятся равномерно в области
, сходятся равномерно в области 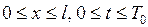 . Можно показать, что при условиях, наложенных выше на функцию
. Можно показать, что при условиях, наложенных выше на функцию 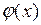 , эти условия выполняются.
, эти условия выполняются.
7.2. Случай неоднородного уравнения.Требуетсянайти функцию 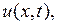 непрерывную при
непрерывную при 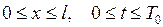 , удовлетворяющую уравнению
, удовлетворяющую уравнению
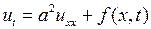 ,
, 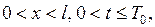 (7.13)
(7.13)
граничным условиям
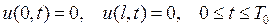 (7.14)
(7.14)
и начальному условию
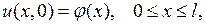 (7.15)
(7.15)
где 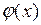 - заданная функция, имеющая непрерывную производную и
- заданная функция, имеющая непрерывную производную и 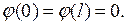
Решение задачи (7.13)- (7.15) будем искать в виде
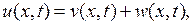 (7.16)
(7.16)
где 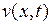 есть решение задачи
есть решение задачи
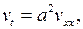 (7.17)
(7.17)
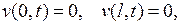 (7.18)
(7.18)
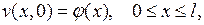 (7.19)
(7.19)
а 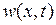 есть решение задачи
есть решение задачи
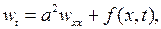 (7.20)
(7.20)
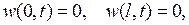 (7.21)
(7.21)
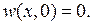 (7.22)
(7.22)
Задача (7.17)- (7.19) для функции 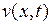 рассмотрена нами в пункте 7.1; ее решение дается рядом (7.10). Решение
рассмотрена нами в пункте 7.1; ее решение дается рядом (7.10). Решение 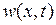 задачи (7.20)- (7.22) будем искать в виде
задачи (7.20)- (7.22) будем искать в виде
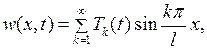 (7.23)
(7.23)
где 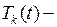 неизвестные функции.
неизвестные функции.
Пусть ряд (7.23) равномерно сходится в области 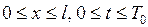 и допускает почленное дифференцирование дважды по
и допускает почленное дифференцирование дважды по 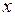 и один раз по
и один раз по 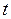 . Тогда, подставляя (7.23) в (7.20), получаем
. Тогда, подставляя (7.23) в (7.20), получаем
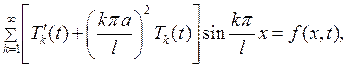
откуда
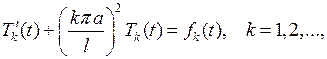 (7.24)
(7.24)
где
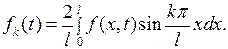 (7.25)
(7.25)
С учетом (7.23) из условий (7.22) получим
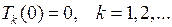 (7.26)
(7.26)
Следовательно, для определения функций 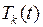 имеем задачу (7.24), (7.26), представляющую задачу Коши для обыкновенного линейного дифференциального уравнения первого порядка (7.24) с начальным условием (7.26). Ее решение дается формулой
имеем задачу (7.24), (7.26), представляющую задачу Коши для обыкновенного линейного дифференциального уравнения первого порядка (7.24) с начальным условием (7.26). Ее решение дается формулой
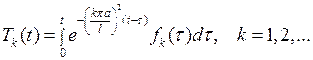 (7.27)
(7.27)
Подставляя в (7.27) вместо 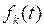 выражение (7.25), а затем полученный результат в (7.23), получаем решение задачи (7.20)- (7.22). Решение исходной задачи (7.13)- (7.15) найдем по формуле (7.16).
выражение (7.25), а затем полученный результат в (7.23), получаем решение задачи (7.20)- (7.22). Решение исходной задачи (7.13)- (7.15) найдем по формуле (7.16).
Решение задачи для уравнения теплопроводности (7.13) в случае неоднородных граничных условий совершенно аналогично соответствующему случаю для уравнения колебаний струны (см. пункт 6.3).
В заключение параграфа отметим, что для уравнения теплопроводности может быть поставлена задача Коши: найти функцию 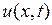 , непрерывную при
, непрерывную при 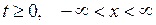 , удовлетворяющую уравнению
, удовлетворяющую уравнению
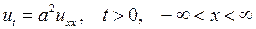
и начальному условию
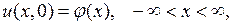
где 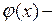 непрерывная и ограниченная функция.
непрерывная и ограниченная функция.
Решение этой задачи Коши дается формулой Пуассона
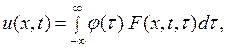
где 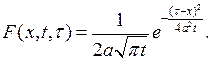
Функция 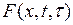 называется фундаментальным решением уравнения теплопроводности.
называется фундаментальным решением уравнения теплопроводности.
Пример 7.1. Решить методом Фурье начально-краевую задачу для однородного уравнения теплопроводности: 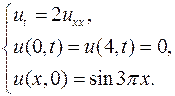
Решение.Решение этой задачи дается формулой (7.10), в которой коэффициенты 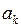 определены соотношениями (7.12). В нашем случае
определены соотношениями (7.12). В нашем случае
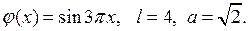 Внося эти данные в (7.12), получаем
Внося эти данные в (7.12), получаем
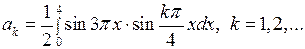
Вычислим интегралы:
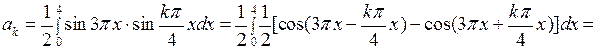
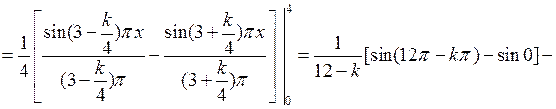
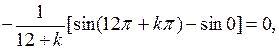 если
если 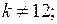
при 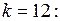
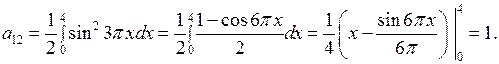
Подставив эти значения коэффициентов 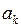 в (7.10), получим решение задачи в следующем виде
в (7.10), получим решение задачи в следующем виде
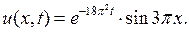
Второй способ нахождения коэффициентов 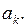 Функцию
Функцию 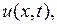 заданную соотношением (7.10), подставим в начальное условие:
заданную соотношением (7.10), подставим в начальное условие:
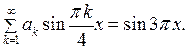
Правая часть этого равенства представляет собой разложение в ряд Фурье по синусам. Поэтому, приравнивая коэффициенты при одинаковых 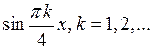 , будем иметь:
, будем иметь: 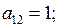 остальные
остальные 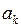 равны нулю.
равны нулю.
Пример 7.2.Решить методом Фурье начально-краевую задачу для неоднородного уравнения теплопроводности
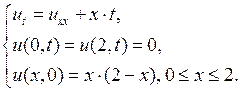
Решение. В соответствии с изложенным в разделе 7.2 §7 решение этой задачи ищется в виде
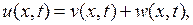 (7.28)
(7.28)
где 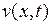 есть решение задачи
есть решение задачи
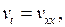
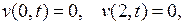
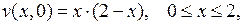
а 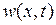 есть решение задачи
есть решение задачи
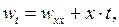
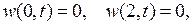
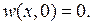
Сначала решаем задачу относительно функции 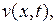 решение которой дается формулой (7.10), в которой коэффициенты
решение которой дается формулой (7.10), в которой коэффициенты 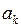 определены соотношениями (7.12). В нашем случае
определены соотношениями (7.12). В нашем случае 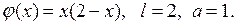 Внося эти данные в (7.12), получаем
Внося эти данные в (7.12), получаем
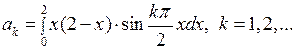
Вычислим эти интегралы с помощью двукратного интегрирования по частям:
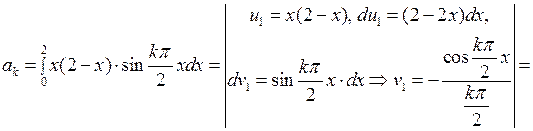
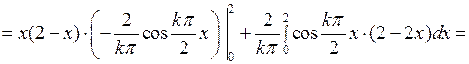
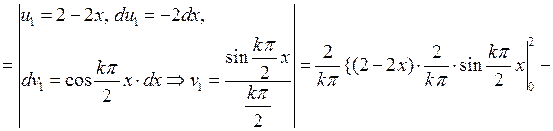
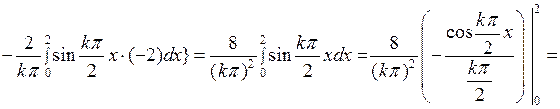
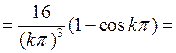
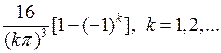
Отсюда видно, что коэффициенты 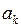 с четными номерами равны нулю. Подставив эти значения коэффициентов
с четными номерами равны нулю. Подставив эти значения коэффициентов 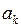 в (7.10), получим решение первой задачи относительно
в (7.10), получим решение первой задачи относительно 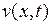 в следующем виде
в следующем виде
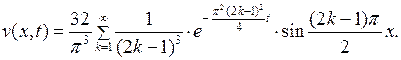 (7.29)
(7.29)
Перейдем к решению задачи относительно функции 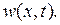 Ее ищем в виде (7.23), где
Ее ищем в виде (7.23), где  и функции
и функции 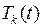 определяются формулой (7.27), которая в нашем случае примет вид:
определяются формулой (7.27), которая в нашем случае примет вид:
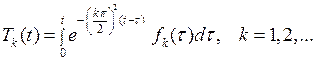 , (7.30)
, (7.30)
где для 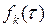 в силу (7.25) с учетом
в силу (7.25) с учетом 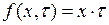 получаем интеграл
получаем интеграл
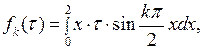 который вычисляется по частям:
который вычисляется по частям:
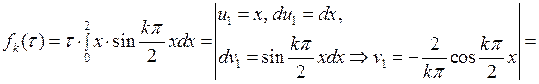
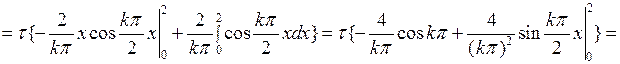
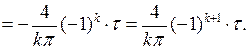
Внося это выражение в (7.30), для 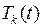 получаем
получаем
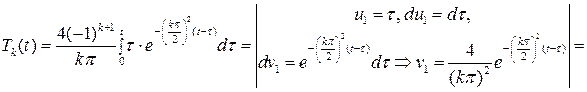
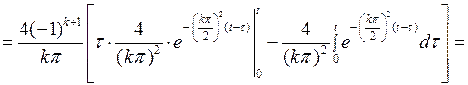
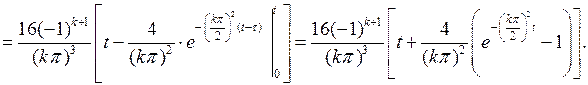
Теперь, если это значение 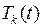 подставить в (7.23), то получим решение второй задачи
подставить в (7.23), то получим решение второй задачи 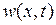 , которое вместе с (7.29) по формуле (7.28) дает решение исходной задачи.
, которое вместе с (7.29) по формуле (7.28) дает решение исходной задачи.
Задачи
Методом Фурье найти решения следующих начально-краевых задач для уравнения теплопроводности:
7.1. 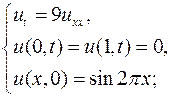 7.2.
7.2. 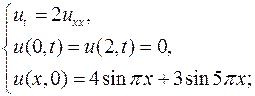
7.3. 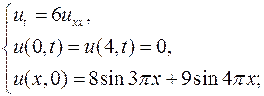 7.4.
7.4. 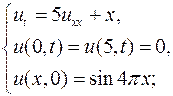
7.5. 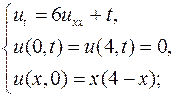 7.6.
7.6. 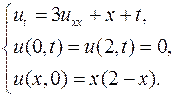
Дата добавления: 2017-03-29; просмотров: 12582;
