Есть канонический вид уравнения эллиптического типа.
Отметим, что рассмотренные в §2 уравнения колебаний струны (2.8), теплопроводности (2.31), Лапласа (2.38) принадлежат соответственно гиперболическому, параболическому и эллиптическому типу.
Отметим также, что классификация дифференциальных уравнений с частными производными производится и в случае, когда число независимых переменных больше двух [1]. Волновое уравнение (2.17), уравнения теплопроводности (2.29) и Лапласа (2.37) принадлежат соответственно гиперболическому, параболическому и эллиптическому типу.
Пример 3.1. Определить тип уравнения
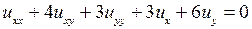
и привести его к каноническому виду.
Решение.Так как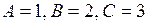 
и 
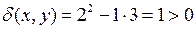, то данное уравнение гиперболического типа. Приведем его к каноническому виду. В соответствии с (3.9) составим характеристическое уравнение
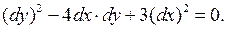
Решаем его. Получаем
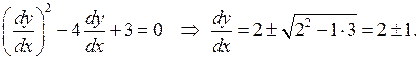
Следовательно, уравнение имеет характеристики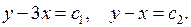 
Поэтому в соответствии с (3.12) положим
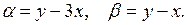
Так как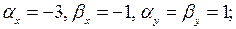 
вторые производные функций 
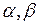равны нулю, то с помощью формул (3.4) получаем
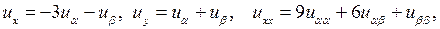
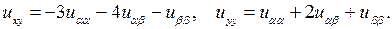
Эти выражения производных подставим в исходное уравнение:
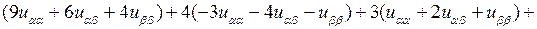
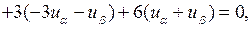
откуда, раскрывая скобки и приводя подобные слагаемые, получаем канонический вид уравнения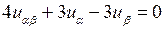 
.
Пример 3.2.Определить тип уравнения
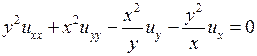
и привести его к каноническому виду.
Решение.Так как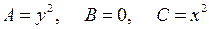 
и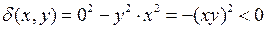 
во всех точках, не лежащих на прямых 
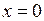или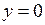 
, то в любом открытом квадранте данное уравнение имеет эллиптический тип. Приведем его к каноническому виду. В соответствии с (3.9) составим характеристическое уравнение
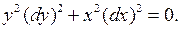
Решаем его. Имеем:
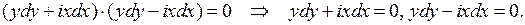
Следовательно, уравнение имеет комплексно сопряженные характеристики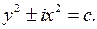 
Поэтому полагаем
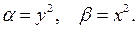
Так как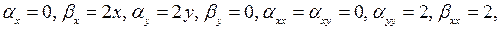 
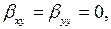то с помощью формул (3.4) находим
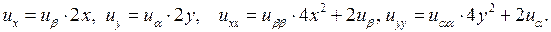
Подставив эти значения в исходное уравнение, получим
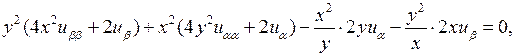
т.е.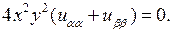 
Сокращая на 
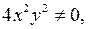приходим к уравнению канонического вида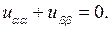 
Пример 3.3.Определить тип уравнения
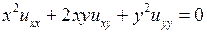
и привести его к каноническому виду.
Решение.Так как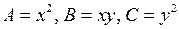 
и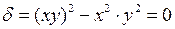 
, то уравнение параболического типа. Приведем его к каноническому виду. Составим характеристическое уравнение
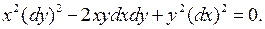
Левая часть этого уравнения есть полный квадрат: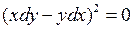 
, откуда 
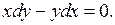Это есть уравнение с разделяющимися переменными.
Решаем его: 
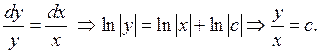
Итак, характеристическое уравнение имеет одно семейство действительных характеристик. Положим
,
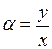а за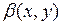 
в соответствии с вышесказанным возьмем любую дважды не-
прерывно дифференцируемую функцию, для которой якобиан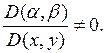 
Например, пусть 
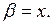Тогда
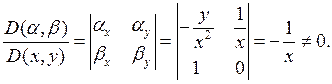
Так как
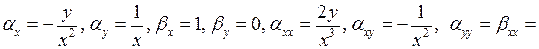
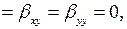то подставляя эти значения производных в (3.4), получаем
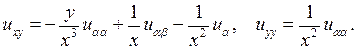
Теперь эти выражения производных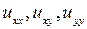 
внесем в исходное уравнение. Получим
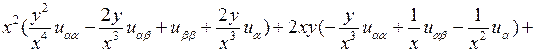
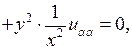
откуда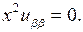 
Сократив на 
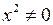, получим канонический вид заданного уравнения: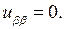 
Задачи
Определить тип уравнений и привести их к каноническому виду.
3.1.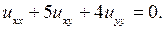 
Ответ: гиперболический,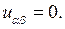 
3.2.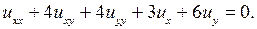 
Ответ: параболический,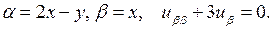 
3.3.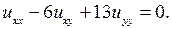 
Ответ: эллиптический,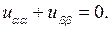
3.4.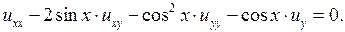 
Ответ: гиперболический,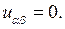
3.5.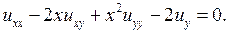 
Ответ: параболический,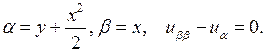 
3.6.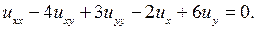 
Ответ: гиперболический,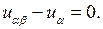 
3.7.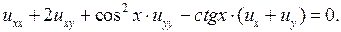 
Ответ: гиперболический,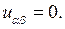
3.8.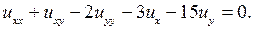 
Ответ: гиперболический,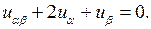 
3.9.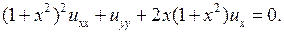 
Ответ: эллиптический,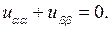
3.10.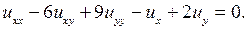 
Ответ: параболический,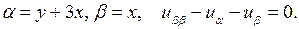 
Дата добавления: 2017-03-29; просмотров: 5417;