Основные дифференциальные уравнения математической физики. Постановка задач

Основные понятия и определения

Уравнение, связывающее независимые переменные 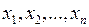, неизвестную функцию 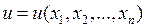и ее частные производные, называется дифференциальным уравнением с частными производными. Оно имеет вид

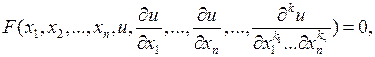(1.1)

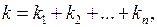
где 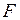- заданная функция своих переменных.

Порядок старшей производной 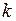, входящей в уравнение (1.1), называется порядком уравнения. Например, уравнение второго порядка 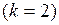с двумя независимыми переменными 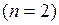имеет вид

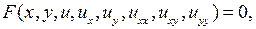(1.2)

где приняты обозначения:

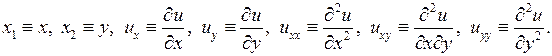
Решением уравнения с частными производными (1.1) называется всякая функция 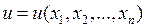, которая, будучи подставлена в уравнение (1.1) вместо неизвестной функции и ее частных производных, обращает это уравнение в тождество по независимым переменным.

Уравнение (1.2) называется линейным относительно старших производных, если оно имеет вид

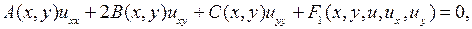(1.3)

где 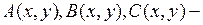известные функции переменных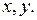

Если коэффициенты 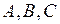зависят не только от 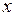и 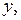но и от 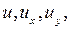то такое уравнение называется квазилинейным.

Уравнение (1.2) называется линейным, если оно линейно как относительно старших производных 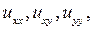так и относительно функции 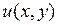и ее первых производных :

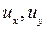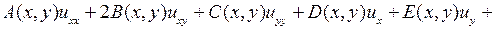
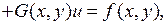(1.4)

где 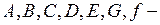известные функции переменных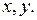

Если 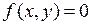, то уравнение (1.4) называется однороднымлинейным дифференциальным уравнением с частными производными второго порядка.

В рамках настоящего учебно-методического пособия мы ограничимся изучением линейных уравнений вида (1.4). Однако, и такие уравнения оказываются еще довольно сложными для исследования и решения. Поэтому в дальнейшем, в основном, будут рассматриваться лишь различные частные случаи уравнения (1.4), которые возникают при описании простейших задач механики и физики.

Основные дифференциальные уравнения математической физики. Постановка задач

Рассмотрим вопрос о том, как проводится исследование физических задач с помощью дифференциальных уравнений с частными производными. Исходным моментом является то, что исследуется не сам реальный физический процесс, а некоторая его модель (идеальный процесс), от которой требуется, чтобы она сохраняла основные черты изучаемого процесса и в то же время была настолько простой, чтобы поддавалась изучению имеющимися математическими методами.

При исследовании идеального процесса можно выделить следующие основные моменты.

1. Выбирается величина 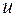(или несколько величин), характеризующая процесс, которая обычно является функцией пространственных переменных 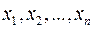и времени :

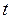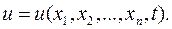
2. На основании законов, которым подчиняется идеальный процесс, выводится дифференциальное уравнение с частными производными относительно функции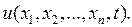

3. Так как дифференциальное уравнение имеет бесчисленное множество решений, то его недостаточно для описания конкретного процесса. Поэтому выводятся еще некоторые дополнительные условия, характеризующие процесс. Такими дополнительными условиями чаще всего являются граничные условия, т.е. условия, заданные на границе рассматриваемой среды, и начальные условия, относящиеся к моменту времени, с которого начинается процесс.

Совокупность дифференциального уравнения и дополнительных условий представляет собой математическую формулировку физической задачи и называется задачей математической физики.

То обстоятельство, что задача математической физики должна отражать (хотя и приближенно) некоторый физический процесс, накладывает на нее ряд требований. А именно, задача считается поставленной корректно (правильно), если ее решение 1) существует, 2) единственно, 3) устойчиво, т.е. малые изменения любого из данных задачи вызывают малое изменение решения. Требование устойчивости необходимо по следующей причине. В данных любой конкретной задачи, полученных из опыта, всегда содержится некоторая погрешность и нужно, чтобы малая погрешность в данных приводила к малой погрешности в решении.

Естественно, что основной проблемой теории «Уравнений математической физики» является нахождение решения задачи математической физики в виде, удобном для практики. Зная это решение 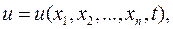можно получить количественную характеристику процесса в любой точке среды и в любой момент времени. В случае, когда решение невозможно найти в явном виде, первостепенное значение приобретает вопрос о его существовании. Очень важны также и вопросы единственности и устойчивости решения.

В настоящем пособии мы ограничимся лишь явным нахождением решений основных задач математической физики, с которыми познакомимся ниже на конкретных примерах.

2.1. Малые поперечные колебания струны.Рассмотрим натянутую струну, закрепленную на концах. Предположим, что в исходном положении струна занимает отрезок 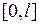оси 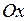. Если ее вывести из положения равновесия, то она будет совершать колебания. Дадим математическую формулировку этому процессу. Примем следующую модель струны: струна есть упругая, невесомая и абсолютно гибкая нить. Таким образом, мы пренебрегаем: а) толщиной струны, б) силами, возникающими при ее изгибании, в) силами тяжести. Оставляем только силы натяжения 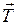, направленные по касательной к струне и подчиненные закону Гука: натяжение струны пропорционально ее удлинению.

Величиной, характеризующей процесс колебания струны, является вектор смещения 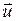точек струны. Предположим, что 1) смещения струны лежат в одной плоскости 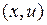и 2) вектор смещения 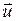перпендикулярен в любой момент к оси 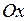(поперечные колебания). Тогда процесс колебания будет характеризоваться одной скалярной величиной 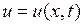- отклонением от положения равновесия точки струны с абсциссой 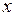в момент времени 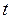. Будем рассматривать малые колебания, т.е. такие, при которых можно пренебрегать квадратом 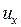по сравнению с единицей.

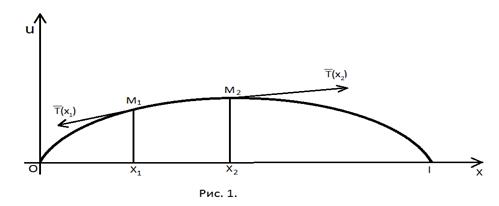
Выделим произвольный участок 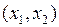струны (рис.1), который при колебании струны деформируется в участок 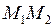. Длина дуги этого участка в момент времени 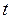равна

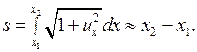
Следовательно, при наших предположениях удлинения струны не происходит и на основании закона Гука величина натяжения 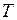в каждой точке струны не меняется со временем. Покажем также, что натяжение не зависит и от 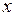, т.е. 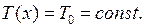С этой целью найдем проекции сил натяжения, действующих на участок 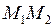, на ос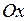и и 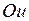(обозначим их 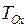и ):

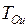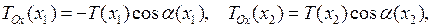
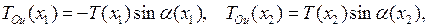(2.1)

где угол между положительным направлением касательной к струне 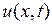в точке с абсциссой 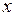и положительным направлением оси .

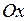Учитывая малость колебаний, в соотношениях (2.1) 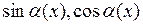можно заменить следующими величинами

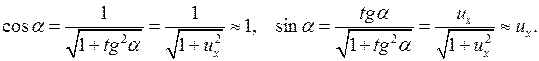(2.2)

На участок 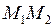струны действуют силы натяжения, внешние силы и силы инерции. На основании принципа Даламбера суммы проекций всех этих сил на ос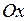и и 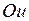должны равняться нулю. Так как мы рассматриваем только поперечные колебания, то силы инерции и внешние силы направлены параллельно оси 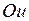. Тогда с учетом соотношений (2.1), (2.2) получим 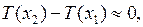откуда в силу произвольности точек 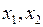следует, что натяжение не зависит от 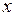, т.е. для всех значени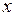й и :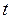

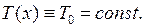
Теперь выведем уравнение колебаний струны. Для этого составим сумму проекций всех сил на ось 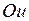. С учетом сказанного выше сумму проекций на ось 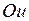сил натяжения запишем в виде

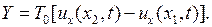
Откуда, замечая, что

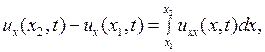
получим

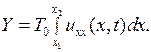(2.3)

Обозначим через 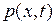внешнюю силу, действующую на струну параллельно оси 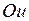и рассчитанную на единицу длины. Тогда проекция на ось 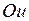внешней силы, действующей на участок 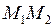струны, будет равна

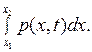(2.4)

Пусть 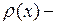линейная плотность струны. Тогда сила инерции участка 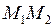струны будет равна

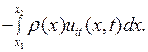(2.5)

Приравнивая к нулю сумму проекций (2.3)-(2.5), получим

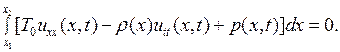(2.6)

Предположим теперь существование и непрерывность вторых производных 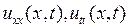, а также считаем функции 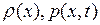непрерывными. Тогда можно показать, что подынтегральное выражение в (2.6) есть тождественный нуль, т.е. имеем

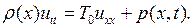(2.7)

Это и есть искомое уравнение колебаний струны.

В случае однородной струны 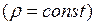уравнение (2.7) обычно записывается в виде

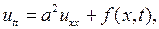(2.8)

где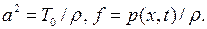

Уравнение (2.8) при 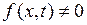называется уравнением вынужденных колебанийструны. При 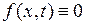(внешняя сила отсутствует) получаем уравнение свободных колебаний струны:

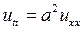. (2.9)

Сформулируем теперь основные дополнительные условия.

1) Концы струны, имеющие абсциссы 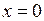и 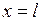, перемещаются по заданному закону:

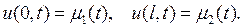(2.10)

Если концы струны жестко закреплены, то

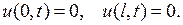(2.11)

2) К концам струны приложены заданные силы:

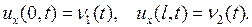(2.12)

Если концы струны свободны, то

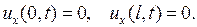(2.13)

3) Концы струны упруго закреплены:

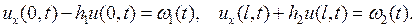(2.14)

В соотношениях (2.10), (2.12), (2.14) справа стоят известные функции, а 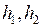в (2.14) - известные положительные постоянные.

Условия (2.10)- (2.14) называются краевыми или граничными условиями. Возможны и другие комбинации граничных условий. Например, один конец струны может перемещаться по заданному закону, а другой конец струны может быть свободным и т.д.

Очевидно, что процесс колебаний будет существенно зависеть также от того, каким способом струна выводится из равновесия. Предположим, что в начальный момент времени 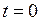всем точкам струны сообщаются некоторые смещения и скорости. Это приводит к следующим условиям:

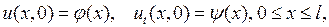(2.15)

где 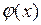и 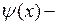заданные функции, выражающие соответственно смещения и скорости точек струны в начальный момент времени.

Условия (2.15) называются начальными условиями, а функции 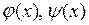- начальными данными.

Таким образом, физическая задача о колебаниях струны свелась к следующей математической задаче:

найти такое решение уравнения (2.7), которое удовлетворяет одному из граничных условий (2.10)- (2.14) и начальным условиям (2.15).

Эта задача называется смешанной задачей, так как включает в себя и граничные, и начальные условия.

Для уравнения (2.7) может быть поставлена и другая задача. Пусть струна достаточно длинная и нас интересует колебание ее точек, достаточно удаленных от концов, причем в течение малого промежутка времени. В этом случае режим на концах не будет оказывать существенного влияния и поэтому его не учитывают; струну же при этом считают бесконечной. Задача ставится так: