Найти решение уравнения (2.7) при так, чтобы оно удовлетворяло начальным условиям

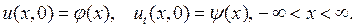(2.16)

Задача (2.7), (2.16) называется задачей Коши.

Уравнение (2.7) описывает колебательные процессы одномерного тела. В трехмерном случае многие колебательные процессы приводят к волновому уравнению

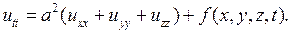(2.17)

Например, к уравнению (2.17) приводят следующие процессы: малые упругие колебания твердых тел, звуковые колебания, электромагнитные колебания.

Уравнение (2.7) является частным случаем уравнения (2.17). Другим частным случаем является уравнение колебаний мембраны

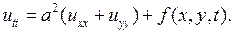(2.18)

К уравнению (2.18) приводят задачи о колебаниях двумерных тел, в частности, задача о малых колебаниях мембраны - свободно изгибающейся упругой пленки.

2.2. Распространение тепла в изотропном твердом теле.Рассмотрим задачу о распространении тепла в неравномерно нагретом твердом теле. За величину, характеризующую процесс, возьмем температуру 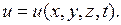Примем следующую модель процесса: происходит механический перенос тепла из мест с более высокой температурой в места с более низкой температурой; все тепло идет на изменение температуры тела; свойства тела от температуры не зависят.

Воспользуемся следующими законами.

1) Закон Фурье: количество тепла 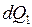, проходящее через элементарную площадку 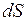внутри тела в направлении нормали 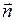к этой площадке за время 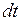, равно

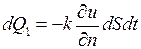, (2.19)

где 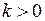- коэффициент внутренней теплопроводности. Будем считать, что тело изотропно в отношении теплопроводности, т.е. 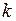зависит только от точки 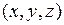тела и не зависит от направления нормали :

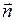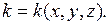
2) Количество тепла 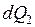, которое получает элементарный объем 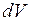за время 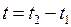, связано с изменением температуры соотношением

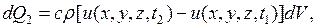(2.20)

где 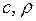- удельная теплоемкость и плотность вещества.

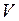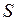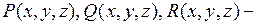Кроме того, нам понадобится формула Остроградского. Пусть - некоторое тело, ограниченное кусочно-гладкой поверхностью , а некоторые функции, непрерывные в 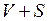и имеющие непрерывные первые производные в 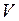. Тогда

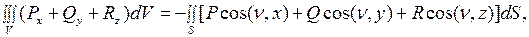(2.21)

где 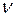- внутренняя нормаль к поверхности .

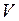Перейдем к выводу уравнения. Выделим внутри рассматриваемого тела произвольный объем , ограниченный поверхностью 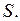В силу формулы (2.19) через поверхность 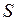за промежуток 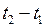объем 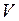получит (или потеряет) количество тепла, равное

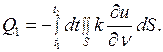(2.22)

Пусть внутри тела имеются источники тепла. Обозначим через 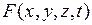плотность этих источников, т.е. количество тепла, выделяемого (или поглощаемого) в единицу времени в единице объема. Тогда количество тепла, выделяемого (или поглощаемого) в объеме 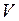за время 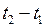, будет равно

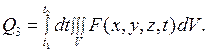(2.23)

Все тепло 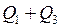пойдет на изменение температуры объема 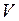. Поэтому с учетом (2.20) может быть записано в виде

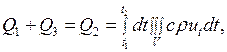(2.24)

при этом нами использовано равенство

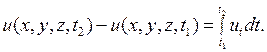
Полагая в (2.21) 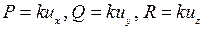, получаем

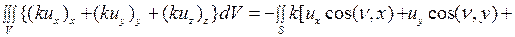
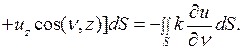(2.25)

С помощью (2.25) выражение (2.22) для 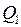можно представить в виде

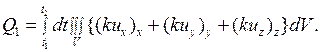(2.26)

Если теперь (2.26) и (2.23) подставить в (2.24), то получим

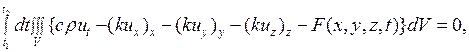
откуда

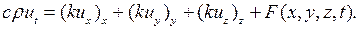(2.27)

Уравнение (2.27) называется уравнением теплопроводности.

Если тело однородно, то 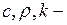постоянные, и уравнение (2.27) примет вид

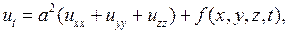(2.28)

где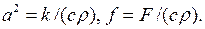

Если в теле нет источников тепла, т.е. 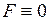, то из (2.28) получаем однородное уравнение теплопроводности

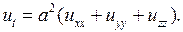(2.29)

В случае двумерного тела, например, при распространении тепла в очень тонкой однородной пластинке, уравнение (2.28) переходит в

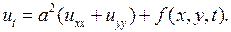(2.30)

Для одномерного тела – тонкого стержня – уравнение (2.28) примет вид

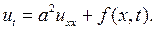(2.31)

При этом предполагается, что грани пластинки и боковая поверхность стержня теплоизолированы.

Рассмотрим теперь дополнительные условия. Из физических соображений следует, что для однозначного определения температуры необходимо знать распределение температуры в начальный момент и тепловой режим на границе 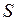тела. Основными видами тепловых режимов являются следующие режимы.

1) На границе поддерживается определенная температура:

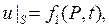(2.32)

где 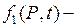известная функция точки 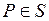и времени .

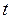2) Через границу 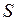подается определенный тепловой поток:

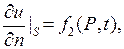(2.33)

где 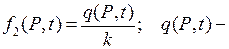плотность теплового потока, т.е. количество тепла, которое получает в единицу времени единица площади поверхности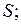 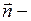внешняя нормаль к 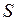; 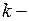коэффициент внутренней теплопроводности.

В частности, если поверхность 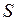теплоизолирована, то

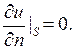
3) Происходит теплообмен между телом и внешней средой, температура которой известна, по закону Ньютона: плотность теплового потока, получаемого телом из внешней среды, равна

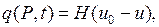
где 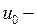температура внешней среды, 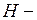коэффициент теплообмена.

В этом случае имеем граничное условие

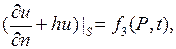(2.34)

где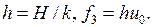

Начальное условие для уравнения теплопроводности (2.27) имеет вид:

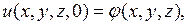(2.35)

где 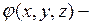заданная функция – температура в начальный момент времени 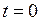в любой точке 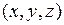тела.

Таким образом, мы приходим к задаче: найти решение уравнения теплопроводности (2.27), удовлетворяющее начальному условию (2.35) и либо условию (2.32) (первая начально-краевая задача), либо условию (2.33) (вторая начально-краевая задача), либо условию (2.34) (третья начально-краевая задача).Совершенно аналогично ставятся задачи в двумерном и одномерном случаях, т.е. для уравнений (2.30), (2.31). Для уравнений (2.27), (2.30),(2.31) можно ставить также и задачу Коши, т.е. задачу без граничных условий.

Отметим, что к уравнению (2.27), помимо задачи о распространении тепла, приводятся и другие физические задачи: диффузия в жидкостях и газах, движение вязкой жидкости и др.

2.3. Установившаяся температура в однородном теле.Рассмотрим частный случай задачи о распространении тепла в однородном теле, когда температура 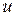не меняется со временем (установившаяся или стационарная температура): 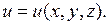Так как в этом случае 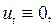то уравнение (2.28) примет вид

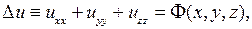(2.36)

где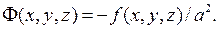

При отсутствии тепловых источников внутри тела ( 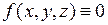) уравнение (2.36) переходит в уравнение

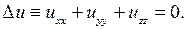(2.37)

Уравнение (2.36) называется уравнением Пуассона, уравнение (2.37) – уравнением Лапласа, оператор 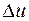- оператором Лапласа.

Для однозначного определения температуры 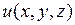теперь не надо задавать начальное ее распределение, а достаточно знать лишь тепловой режим на границе 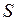тела. В результате приходим к следующим задачам: внутри поверхности 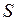найти решение уравнения (2.36) или (2.37), удовлетворяющее на границе 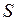тела либо условию (2.32) (задача Дирихле), либо условию (2.33) (задача Неймана), либо условию (2.34) (третья краевая задача или задача с косой производной).

Совершенно аналогично получаем двумерные уравнения Пуассона и Лапласа:

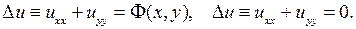(2.38)

Граничные условия для этих уравнений задаются на замкнутой плоской кривой.

К граничным задачам для уравнений Пуассона и Лапласа, помимо задачи об установившейся температуре, приводятся многие стационарные задачи из электростатики, магнитостатики, гидродинамики и других разделов естествознания.