С явными потерями и примитивным потоком вызовов

Рассмотрим однозвенную неблокирующую коммутационную схему, на которую поступает примитивный поток вызов с параметром 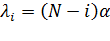, дисциплина обслуживания - с явными потерями.

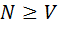
Время обслуживания одного вызова – случайная величина, распределенная по показательному закону со средним значением, принятым за единицу времени 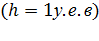,т.е.

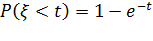
Требуется определить вероятность возможных состояний полнодоступного пучка в процессе обслуживания поступающих вызовов, если число занятых линий 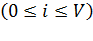-состояния коммутационной системы .

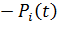При поступлении вызова или окончания занятия, коммутационная система скачкообразно переходит из одного состояния в другое. Допустим, что в момент времени 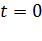известно i-ое состояние коммутационной системы либо распределение вероятностей состояния 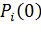.Возникает задача: найти распределение .

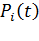Возьмем на оси времени временной отрезок длиной и выделим на нем бесконечно малый промежуток 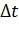. В состояние коммутационная система могла перейти из какого-то состояния 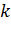за промежуток времени .

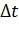Вероятность перехода коммутационной системы из состояния 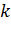в состояние за промежуток времени 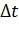, оценивается с помощью переходной вероятности 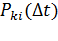. Тогда уравнение для вероятностей состояния системы будет иметь вид (5.1).

Используя уравнение Колмогорова - Чепмена , составляется выражение для определения 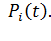С учетом определения параметра потока и выполняя соответствующие математические преобразования, получим систему уравнений:

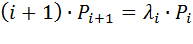. (5.16)

Из выражения (5.16) выразим вероятность :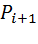

(5.17)

Будем подставлять в (5.16) вместо :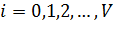

- : ; ;

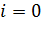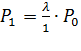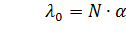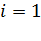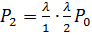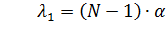- : ; и т.д.

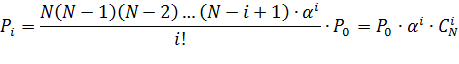
Используя формулу (2.9) можно записать:

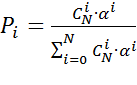(5.18)

Формула (5.18) носит название - распределение Энгсета.

Выражение (5.18) является более общим по сравнению с выражением (5.8) и в предельном случае при 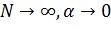распределение Энгсета переходит в распределение Эрланга.