Характеристики качества обслуживания
1. Вероятность потерь по времени. Формула для определения вероятности потерь по времени получается непосредственно из выражения (5.8), если 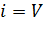 .
.
При выводе выражения (5.8) было сделано допущение 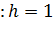 , т.е.
, т.е. 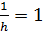 , поэтому можно записать:
, поэтому можно записать:
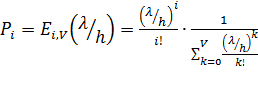 (5.9)
(5.9)
Учитывая, что поступающий поток простейший, для которого 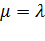 , выражение (5.9) примет вид:
, выражение (5.9) примет вид:
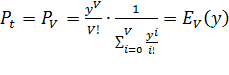 (5.10)
(5.10)
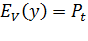 - компактная формула записи первой формулы Эрланга, то есть
- компактная формула записи первой формулы Эрланга, то есть
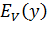 - вероятность потерь в пучке из
- вероятность потерь в пучке из 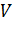 линий, на который поступает нагрузка
линий, на который поступает нагрузка 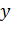 .
.
Формула (5.10) была выведена Эрлангом в 1917г. Иногда ее называют
В-формула Эрланга. Позже Б.А. Севастьяновым было доказано, что соотношение, полученное Эрлангом, справедливо для любого закона распределения длительности обслуживания вызовов.
Учитывая определение простейшего потока, можно утверждать, что
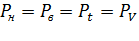 .
.
Формула (5.10) табулирована: составлены таблицы, определяющие зависимости между 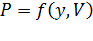 - таблицы Пальма.
- таблицы Пальма.
Часто в инженерных расчетах удобно пользоваться рекуррентной формулой:
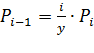 (5.11)
(5.11)
2.Интенсивность пропущенной нагрузки.Если известна величина поступающей нагрузки 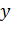 , емкость пучка
, емкость пучка 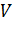 , вероятность потерь
, вероятность потерь  , можно записать:
, можно записать:
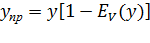 (5.12)
(5.12)
или
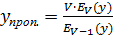 (5.13)
(5.13)
3.Пропускная способность отдельных линий пучка.Занятие линий в пучке может быть:
3.1) упорядоченным, когда первой всегда занимается линия с меньшим номером;
3.2) случайным, когда занимается любая свободная линия пучка..
При случайном искании, т. к. занимается любая свободная линия, то
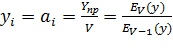 (5.14)
(5.14)
При упорядоченном искании:
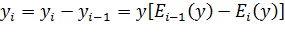 (5.15)
(5.15)
4.Математическое ожидание и дисперсия пропущенной нагрузки. Так как поступающая нагрузка имеет Пуассоновское распределение, то ее математическое ожидание и дисперсия одинаковы и равны 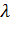 .
.
Дата добавления: 2017-02-20; просмотров: 595;
