Критерий Колмогорова-Смирнова.
критерия Колмогорова-Смирнова. При использовании критерия должны выполняться следующие условия:
1) обе выборки случайные;
2) выборки независимы, и члены каждой выборки независимы между собой;
3) изучаемое свойство имеет непрерывное распределение в обеих совокупностях, из которых сделаны выборки;
4) шкала измерений не ниже порядковой.
b) Проверке подлежит гипотеза H0: F(x)=G(x), или предположение об одинаковых функциях распределения баллов за проверочную работу, среди студентов, обучавшихся по различным методикам. Альтернативная гипотеза H1: F(x)≠G(x) предполагает, что функции распределения баллов за проверочную работу различны.
c) Результаты проверочной работы запишем в форме интервальных рядов. Величину интервала выберем равной 10.
d) Подсчитаем число наблюдений, попавших в каждый из этих интервалов, по каждой выборке в отдельности и составим таблицу (таблица 25):
e) Таблица 25.
f) Расчётная таблица критерия Колмогорова-Смирнова
| интервал | Частота в первой выборке | Частота во второй выборке | Накопленная частота в первой выборке | Накопленная частота во второй выборке | Эмирическая функция распределения S1(x) | Эмпирическая функция распределения S2(x) | S1(x)-S2(x) | |S1(x)-S2(x)| | S2(x)-S1(x) |
| 1-10 | |||||||||
| 11-20 | 0,02 | -0,02 | 0,02 | 0,02 | |||||
| 21-30 | 0,02 | 0,08 | -0,06 | 0,06 | 0,06 | ||||
| 31-40 | 0,06 | 0,23 | -0,17 | 0,17 | 0,17 | ||||
| 41-50 | 0,14 | 0,33 | -0,19 | 0,19 | 0,19 | ||||
| 51-60 | 0,32 | 0,60 | -0,28 | 0,28 | 0,28 | ||||
| 61-70 | 0,54 | 0,79 | -0,25 | 0,25 | 0,25 | ||||
| 71-80 | 0,86 | 0,92 | -0,06 | 0,06 | 0,06 | ||||
| 81-90 | 0,92 | 0,98 | -0,06 | 0,06 | 0,06 | ||||
| 91-100 | 1,00 | 0,00 | 0,00 | 0,00 | |||||
| 0,28 | 0,28 | 0,28 |
g)
h)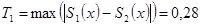 
, 
, 
.
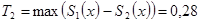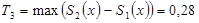i) Следовательно,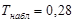 
.
j) Критическое значение критерия находим по формуле: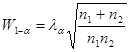 
, где 
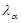- квантиль Колмогорова, отвечающий выбранному уровню значимости. При α=0,05 
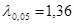[38, стр.115]. Находим 
.
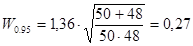k) Отсюда верно неравенство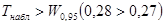 
. В связи с правилом принятия решения [38, стр. 113, случай а] нулевая гипотеза отклоняется и принимается альтернативная гипотеза Н1, что говорит о различии распределений числа баллов за проверочную работу среди групп студентов обучающихся по различным методикам. Анализ экспериментальных данных, приведенных в таблице 25 позволяет уточнить полученный вывод, так как даёт основания утверждать, что студенты, обучающиеся в экспериментальной группе, дают стохастически лучшие результаты, т.е. изучение основ теории вероятностей и математической статистики с использованием контекстных задач является более эффективным, по отношению к традиционной методике.
l) На основании положительной динамики результатов педагогического эксперимента можно сделать вывод, что предлагаемая нами методика способствует повышению уровня обучаемости, сформированности знаний и умений по теории вероятностей и математической статистике, а также обеспечивает повышение степени обученности студентов.
Дата добавления: 2019-10-16; просмотров: 852;