Ограничения критерия
1. В каждой из сопоставляемых выборок должно быть не менее 11 наблюдений. При этом объемы выборок должны примерно совпадать.
2. Диапазоны разброса значений в двух выборках должны не совпадать между собой, в противном случае применение критерия бессмысленно.
Между тем, возможны случаи, когда диапазоны разброса значений совпадают, но, вследствие разносторонней асимметрии двух распределений, различия в средних величинах признаков существенны.
Алгоритм
Подсчет критерия Q–Розенбаума
1. Проверить, выполняются ли ограничения: 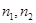 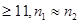 .
2. Упорядочить значения отдельно в каждой выборке по степени возрастания
признака. Считать выборкой 1 – ту выборку, значения в которой предположительно выше, а выборкой 2 – ту, где значения предположительно ниже.
3. Определить самое высокое значение в выборке 2.
4. Подсчитать количество значений в выборке 1, которое выше максимального значения в выборке 2. Обозначить полученную величину как S1.
5. Определить самое низкое значение в выборке 1.
6. Подсчитать количество значений в выборке 2, которые ниже минимального значения выборки 1 . Обозначим полученную величину как S2.
7. Подсчитать эмпирические значение Q по формуле: Q = S1 + S2.
8. По таблице 5 (приложение) определить критические значения Q для данных n1 и n2. Если Qэмп. равно Q0.05 или превышает его, Н0 отвергается.
9. При n1,n2>26 сопоставить полученное эмпирическое значение с Qкр= 8 ( .
2. Упорядочить значения отдельно в каждой выборке по степени возрастания
признака. Считать выборкой 1 – ту выборку, значения в которой предположительно выше, а выборкой 2 – ту, где значения предположительно ниже.
3. Определить самое высокое значение в выборке 2.
4. Подсчитать количество значений в выборке 1, которое выше максимального значения в выборке 2. Обозначить полученную величину как S1.
5. Определить самое низкое значение в выборке 1.
6. Подсчитать количество значений в выборке 2, которые ниже минимального значения выборки 1 . Обозначим полученную величину как S2.
7. Подсчитать эмпирические значение Q по формуле: Q = S1 + S2.
8. По таблице 5 (приложение) определить критические значения Q для данных n1 и n2. Если Qэмп. равно Q0.05 или превышает его, Н0 отвергается.
9. При n1,n2>26 сопоставить полученное эмпирическое значение с Qкр= 8 ( 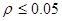 ) и Qкр= 10 ( ) и Qкр= 10 ( 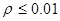 ). Если Qэмп. превышает или по крайней мере равняется Qкр= 8, Н0 отвергается. ). Если Qэмп. превышает или по крайней мере равняется Qкр= 8, Н0 отвергается.
|
Дата добавления: 2019-10-16; просмотров: 566;
