В. Постановка задачи и выбор критерия оптимизации парка машин.
Пусть известны:
– структура производственной программы;
– физические объемы работ на планируемых к выполнению объектах строительства, их технологическая структура;
– возможные средства механизации для выполнения работ и условия их использования;
– годовая выработка каждой машины;
– удельные приведенные затраты при работе на каждом объекте строительства.
Требуется определить, какие типоразмеры машин и в каком количестве необходимо иметь, чтобы минимизировать суммарные приведенные затраты на выполнение всех запланированных объектов строительства.
Выявление основных особенностей, взаимосвязей и количественных закономерностей.
Для строительства характерно очень большое разнообразие объектов. В целях сокращения имеющегося разнообразия, используя определенные методы, например кластерный анализ, выделяют объекты-представители, которые характеризуют некоторую группу объектов.
Но даже при выделении объектов-представителей их число может быть также большим.
Идеальным случаем с точки зрения минимизации текущих эксплуатационных затрат без учета амортизационных затрат на реновацию было бы использование специализированных средств механизации, ориентированных на свой объект строительства, однако создание и производство большого числа типоразмеров машин связано с увеличением капитальных вложений на их создание и производство.
Принятые обозначения:
ai – объем работ, выполняемый Аi – м типоразмером машин; m – число принятых к расчету типоразмеров машин;
Обозначим через bj – объем работ на Bj – м объекте строительства, n – число объектов строительства через n.
Обозначим соответственно yij – удельные приведенные затраты; и хij – объем работ, выполняемый Аi – м типоразмером машин на Bj – м объекте.
ai – объем работ, выполняемый Аi – м типоразмером машин;
m – число принятых к расчету типоразмеров машин;
bj – объем работ на Bj – м объекте строительства,
n – число объектов строительства
yij – удельные приведенные затраты;
хij – объем работ, выполняемый Аi – м типоразмером машин на Bj – м объекте.
Пгij – годовая выработка Аi – го типоразмера машины на Bj – м объекте.
При невозможности использования тех или иных машин на каких-либо объектах, например крана с малой высотой подъема груза при строительстве высотных сооружений, размер удельных приведенных затрат принимается очень большим, чтобы исключить возможность использования таких машин на соответствующих объектах.
Объемы работ выполняемые каждым типоразмером машин, должны удовлетворять следующему равенству
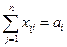 ( i=1,2,…,m)
( i=1,2,…,m)
m – число типоразмеров машин.
Капитальные вложения на создание и производство средств механизации существенно зависят от серийности выпуска и, как правило, эти затраты нелинейно зависят от числа выпускаемых машин.
Серийность выпуска определяется потребностью. А потребность в машинах определяется исходя из минимума суммарных затрат на создание, производство и эксплуатацию машин.
Получается своего рода замкнутый круг. Чтобы выйти из него существует много способов. Рассмотрим оптимизацию парка машин на упрощенном примере (табл. 1).
Таблица 1 – Матрица затрат – исходные данные.
| Типоразмеры машин Аi | Удельные приведенные затраты yij по объектам Bj | Объем работ выполняемый Аi – м типоразмером машин ai | |||
| В1 | В2 | В3 | В4 | ||
| А1 А2 А3 А4 | |||||
| Объем работ на Bi – м объекте bj | – |
Построение математической модели.
Математическая модель оптимизации парка машин записывается в таком виде:
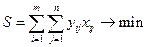
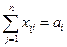 (i = 1,2,…,m)
(i = 1,2,…,m)
При решении задачи оптимизации парка машин имеется много неопределенностей.
Во-первых, искомый типоразмерный ряд машин неизвестен. Во-вторых, объемы работ, выполняемые каждым типоразмером машин, неизвестны и, кроме того, неизвестны объемы работ, выполняемые каждым типоразмером машин на каждом объекте строительства.
Алгоритм оптимизации.
Эффективность оптимизации парка СДМ существенно зависит от принятого алгоритма оптимизации.
В основу алгоритма положено комбинированное использование одного из методов решения транспортной задачи (локальная оптимизация) и метод случайного поиска (глобальная оптимизация) с определенными числами итераций (повторений) на различных стадиях оптимизации для учета следующих нелинейностей:
– серийности выпуска машин,
– снижения затрат на эксплуатацию машин при уменьшении числа используемых типоразмеров машин и др.
Алгоритм оптимизации парка машин включает следующие основные этапы:
1) определение начального (исходного) типоразмерного ряда машин.
Он может быть похож на существующий, может быть расширен, сужен исходя из эвристических соображений или на основании определенных тенденций, опыта, экспертных оценок и т. д.;
2) определение начальных (исходных) объемов работ, выполняемых каждым Аi – м типоразмером машин, удовлетворяя условию,
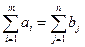
Начальное распределение объемов работ может быть проведено равномерно, случайным образом или с использованием каких-либо других соображений.
В данной задаче приняты начальные объемы работ равными: а1 = 14, а2 = 20, а3 = 26, а4 = 41;
3) Определение усредненной годовой выработки каждым Аi – м типоразмером машин Пгi.
Для этого априорно назначаются вероятности использования каждого типоразмера машин на каждом объекте
Пгi 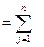 ПгijPij , (i = 1,2,…,m)
ПгijPij , (i = 1,2,…,m)
где Pij – априорная вероятность использования Аi – го типоразмера машин на Bj – м объекте;
Пгij – годовая выработка Аi – го типоразмера машин на Bj – м объекте;
4) определение усредненного числа машин Аi – го типоразмера:
Ni = ai /Пгi , (i = 1,2,…,m)
5) определение удельных приведенных затрат для каждого Аi – го типоразмера машин при работе на Bj – м объекте с учетом серийности выпуска машин.
Для сокращения объема вычислений целесообразно удельные приведенные затраты yij представить в виде 2-х слагаемых:
1-е слагаемое – это затраты, не зависящие от серийности выпуска машин yij,1, и затраты зависящие от серийности yij,2;
6) определение оптимальных объемов работ хij , выполняемых каждым типоразмером машин на каждом объекте, используя один из методов решения транспортной задачи.
Транспортная задача формулируется так:
Имеется m типоразмеров машин (пунктов отправления) А1, А2,…,Аm и n объектов строительства (пунктов назначения) В1, В2,…,Вn .
Известны затраты yij на выполнение единицы работы каждым типоразмером машин на каждом объекте (затраты на перевозку груза из каждого пункта отправления в каждый пункт назначения).
Требуется определить, какой объем работ (количество груза) хij необходимо выполнить (перевезти) каждым типоразмером машин (из каждого пункта отправления) на каждом объекте строительства (в каждый пункт назначения) чтобы:
– выполнить все объемы работ, которые соответствуют каждому типоразмеру машин (вывезти все грузы всех отправителей);
– выполнить все объемы работ на объектах строительства (удовлетворить всех потребителей грузов);
– минимизировать суммарные затраты на выполнение всех объемов работ (на перевозку всех грузов).
Разработано несколько алгоритмов решения транспортной задачи.
Рассмотрим два из них:
– метод Фогеля – приближенный метод решения транспортной задачи;
– методом дефектов – точным методом, обеспечивающим повышенное быстродействие при решении на ЭВМ;
7) определение суммарных приведенных затрат на выполнение заданных объемов работ Bj (j = 1,2,…,n)
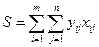
8) определение уточненной годовой выработки каждым типоразмером машин на каждом объекте. Для этого используются оптимальные объемы работ, определенные в результате решения транспортной задачи – этап 6;
9) определение уточненного количества машин Аi – го типоразмера
Ni = 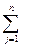 хij / Пгij
хij / Пгij
10) определение удельных приведенных затрат для каждого Аi – го типоразмера машин при работе на Bj – м объекте с учетом уточненной серийности выпуска машин, т. е. корректируются затраты, зависящие от серийности машин yij,2;
11) проверка окончания первого цикла расчетов.
Если значения разности удельных приведенных затрат для 2-х смежных итераций не превышает заданной точности. То переходят к следующему этапу в противном случае возвращаются к этапу 0.
12) запоминание результатов локальной оптимизации.
Из результатов локальной оптимизации на двух смежных итерациях запоминается тот локальный оптимальный парк Ni (i = 1,2,…,m) и суммарные приведенные затраты S, которым соответствуют минимальные суммарные приведенные затраты на выполнение всего объема работ;
* итерация (повторение) – результат повторного применения какой-либо математической операции.
13) определение оптимального парка машин для расчетного типоразмерного ряда машин.
Если число выполненных итераций для поиска оптимального парка при изменении объема работ, выполняемых каждым типоразмером машин, не превышает заранее заданное, то переходят к следующему этапу, в противном случае переходят к этапу 15;
14) определение объемов работ выполняемых каждым Аi – м типоразмером машин.
Объемы работ распределяются по всем типоразмерам машин случайным образом с использованием датчика случайных чисел с заданным или принятым законом распределения.
В рассматриваемой задаче примем равномерный закон распределения. В качестве датчика случайных чисел обычно используют специализированные подпрограммы.
При этом должно удовлетворяться условие
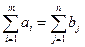
15) определение оптимального парка.
Если число выполненных итераций, предусмотренных при изменении типоразмерного ряда, не превышает заранее заданное, то переходят к следующему этапу, в противном случае имеем искомый оптимальный парк машин;
16) определение нового типоразмерного ряда машин.
Для этого может быть использован датчик случайных чисел или другие способы. После этого переходят к этапу 3.
В. Оптимизация парка СДМ на основе метода Фогеля.
На начальных этапах оптимизации парка машин можно использовать приближенный метод Фогеля, который дает решение, наиболее близкое к оптимальному.
Эвристический метод Фогеля использует концепцию штрафов за отказ от использования наиболее экономичных типоразмеров машин.
Для каждого типоразмера машин вычисляется минимальный штраф за отказ использовать его на наиболее выгодном объекте. Затем среди вычисленных значений минимального штрафа определяется наибольший и выбирается соответствующий этому значению типоразмер машины и объект его работы. Наиболее эффективному типоразмеру машины выделяется (назначается) максимально допустимый объем работ.
Смысл такого распределения в том, что оно позволяет избежать наибольшего из минимальных значений штрафа.
Если годовая выработка выбранного типоразмера машин исчерпана, то этот типоразмер машин исключается из дальнейшего рассмотрения, аналогично исключается и объект на котором выполнен годовой объем работ.
Данная процедура повторяется до тех пор, пока не будут выполнены все объемы работ на всех объектах.
Штраф для каждого типоразмера машин или объекта равен разности между двумя минимальными стоимостями.
Алгоритм метода включает следующие основные этапы:
1) вычисление разностей в каждой строке и в каждом столбце матрицы затрат (табл. 1) между меньшей стоимостью и ближайшей к ней по величине.
Эти разности соответствуют штрафам, которые записываются справа в столбцах разностей (штрафов), разности по столбцам (штрафы по столбцам) записываются внизу в строках разностей.
Например, на первой итерации для строки А1 разность равна
А1В2 – А1В3 = 38 –24 = 14 и т. д.,
Для столбца В1 разность равна
А3В1 – А4В1 = 19 – 3 = 16 и т. д.
2) поиск из всех разностей максимальной, как по строкам, так и по столбцам.
В данном примере максимальная разность на первой итерации равна 38 и находится в строке А2 .
Подчеркнем максимальную разность. Если имеется несколько максимальных разностей (минимальных штрафов), то подчеркивается любая из них;
3) поиск в строке (столбце) с максимальной разностью клетки с наименьшей стоимостью и направление в нее максимально возможного количества ресурсов.
В рассматриваемом примере максимальная разность соответствует строке А2 , ищем в этой строке клетку с минимальной стоимостью – это клетка А2В2 . Направляем в эту клетку максимально возможное количество ресурсов.
Максимально возможное количество ресурсов, направляемое в клетку, определяется как меньшее число из имеющихся на данной итерации ресурсов у соответствующего отправителя и потребителя.
В нашем примере на первой итерации отправитель А2 имеет 20 ед. ресурсов, а потребитель В2 – 22 ед. ресурсов.
В клетку А2В2 направляем меньшее число, т. е. 20 ед. ресурсов.
Поскольку все ресурсы отправителя полностью исчерпаны, строку А2 исключаем из дальнейших расчетов, для чего отметим все клетки этой строки звездочками *. На каждой итерации одна из строк или столбцов, реже и строка и столбец, исключается из дальнейших расчетов, что упрощает с каждой итерацией расчет разностей по строкам и столбцам.
4) Вычисление разностей в каждой строке и в каждом столбце матрицы затрат между наименьшей стоимостью и ближайшей к ней по величине, не принимая во внимание клетки с распределенными в них ресурсами и отмеченные звездочкой.
В нашем примере это, по существу, будет вторая итерация (см. пункт 1).
Так, для строки А1 разность равна А1В2 – А1В3 = 38 – 24 = 14 , т. е. разность по величине осталась прежней. А для столбца В2 разность равна
А4В2 – А3В2 = 36 – 10 = 26,
т. е. по сравнению с первой итерацией изменилась, так как из рассмотрения была исключена клетка А2В2 , в которую на первой итерации были распределены ресурсы: поиск из всех разностей максимальной, как по строкам, так и по столбцам.
5) переход к этапу 2)
Этапы 2), 3), 4) выполняются до тех пор, пока все ресурсы отправителей и потребителей не будут распределены.
Если объемы работ по столбцу не выполнены, то находится следующая клетка с минимальным элементом в этом столбце, куда и распределяются оставшиеся объемы работ, и так до выполнения работ по столбцу.
И если объем работ полностью выполнен по столбцу, то переходят к соседнему столбцу В2 и т. д.
Число итераций выполняемых методом Фогеля, определяется выражением
( М + N – 3) = 4 +4 –3 = 5
М – число принятых к расчету типоразмеров машин;
N – число машин;
Суммарные затраты на транспортировку ресурсов из каждого пункта отправления в каждый пункт назначения
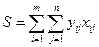 = 23·19 + 7·3 + 20·18 + 2·10 + 14·24 + 1·100 + 34·8 = 1546
= 23·19 + 7·3 + 20·18 + 2·10 + 14·24 + 1·100 + 34·8 = 1546
В результате расчетов получили оптимальное распределение объемов работ (табл. 3).
Таблица 3 – Оптимальное распределение объемов работ
| Типоразмеры машин Аi | Объемы работ аi по объектам Вj | |||
| В1 | В2 | В3 | В4 | |
| А1 | ||||
| А2 | ||||
| А3 | ||||
| А4 |
Таблица 2 – матрица затрат – исходные данные
| Типоразмеры машин Аi | Удельные приведенные затраты yij по объектам Bj | Объем работ выполняемый Аi – м типоразмером машин ai | Номер итерации | |||||||
| В1 | В2 | В3 | В4 | |||||||
| Столбцы разностей (штрафов) | ||||||||||
| А1 | – | – | – | |||||||
| А2 | 58* | 18* | 56* | 72* | – | – | – | – | ||
| А3 | ||||||||||
| А4 | 8 34 | |||||||||
| Объем работ на Bi – м объекте bj | ||||||||||
| Номер итерации | Строки разностей (штрафы по столбцам) | |||||||||
| – | ||||||||||
| – | – |
Дата добавления: 2017-03-29; просмотров: 1306;
