Назначение критерия
Критерий 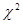 применяется в двух целях:
применяется в двух целях:
1) для сопоставления эмпирического распределения признака с теоретически-равномерным, нормальным или каким-то иным;
2) для сопоставления двух, трех или более эмпирических распределений одного и того же признака.
Описание критерия
Критерий 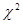 отвечает на вопрос о том, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределениях или в двух и более эмпирических распределениях.
отвечает на вопрос о том, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределениях или в двух и более эмпирических распределениях.
Преимущество метода состоит в том, что он позволяет сопоставлять распределения признаков, представленных в любой шкале, начиная от шкалы наименований. В самом простом случае альтернативного распределения «да – нет», «решил задачу – не решил задачу» и т. п. мы уже можем принимать критерий 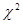 .
.
Мы можем сопоставлять распределения выборов из трех и более альтернатив. Например, если в выборке из 50 человек, 30 выбрали ответ (а), 15 – ответ (б) и 5 – ответ (в), то мы можем с помощью метода 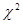 проверить, отличается ли это распределение от равномерного распределения или от распределения ответов в другой выборке, где ответ (а) выбрали 10 человек, ответ (б) – 25 человек, ответ (в) – 15 человек.
проверить, отличается ли это распределение от равномерного распределения или от распределения ответов в другой выборке, где ответ (а) выбрали 10 человек, ответ (б) – 25 человек, ответ (в) – 15 человек.
При сопоставлении двух эмпирического распределения с теоретическим мы определяем степень расхождения между эмпирическими и теоретическими частотами.
При сопоставлении двух эмпирических распределений мы определяем степень расхождения между эмпирическими частотами и теоретическими частотами, которые наблюдались бы в случае совпадения двух этих эмпирических распределений. Формулы расчета теоретических частот будут специально даны для каждого варианта сопоставлений.
Чем больше расхождение между двумя сопоставлениями распределения, тем больше эмпирическое значение 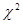 .
.
Гипотезы
Возможно два варианта гипотез, в зависимости от задач, которые мы перед собой ставим.
Первый вариант
Н0: Полученное эмпирическое распределение признака не отличается от теоретического распределения
Н1: Полученное эмпирическое распределение признака отличается от теоретического распределения
Второй вариант
Н0: Эмпирическое распределение 1 не отличается от эмпирического распределения 2
Н1: Эмпирическое распределение 1 отличается от эмпирического распределения 2
Ограничения критерия
1. Объем выборки должен быть достаточно большим: n 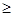 30. При n < 30 критерий
30. При n < 30 критерий 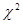 дает весьма приближенные значения. Точность критерия повышается при большихn.
дает весьма приближенные значения. Точность критерия повышается при большихn.
2. Теоретическая частота для каждой ячейки не должна быть меньше 5. Это означает, что если число разрядов задано заранее и не может быть изменено, то мы не можем применять метод 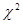 , не накопив определенного минимального числа наблюдений.
, не накопив определенного минимального числа наблюдений.
3. Выбранные разряды должны «вычерпывать» все распределение, то есть охватывать весь диапазон вариативности признаков. При этом группировка на разряды должна быть одинаковой во всех сопоставляемых распределениях.
4. Необходимо вносить «поправку на непрерывность» при сопоставлении распределений признаков, которые принимают всего 2 значения.
5. Разряды должны быть неперекрещивающимися: если наблюдение отнесено к одному разряду, то оно уже не может быть отнесено ни к какому другому разряду.
6. Сумма наблюдений по разрядам всегда должна быть равна общему
количеству наблюдений.
Расчет данного критерия, сможем провести с помощью алгоритма.
Алгоритм
Расчет критерия 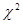 1. Занести в таблицу наименования разрядов и соответствующие им частоты
контрольной (n1) и экспериментальной (m1) групп.
2. Определить число степеней свободы по формуле:
1. Занести в таблицу наименования разрядов и соответствующие им частоты
контрольной (n1) и экспериментальной (m1) групп.
2. Определить число степеней свободы по формуле: 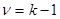 , где k – количество разрядов признака.
3. Посчитать по формуле: , где k – количество разрядов признака.
3. Посчитать по формуле: 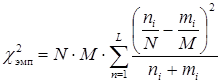 , где , где 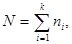 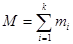 4. Определить по таблице 4 (приложение) критические значения для данного числа степеней свободы
4. Определить по таблице 4 (приложение) критические значения для данного числа степеней свободы 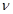 .
Если .
Если 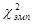 меньше критического значения, расхождения между распределениями статистически недостоверны.
Если меньше критического значения, расхождения между распределениями статистически недостоверны.
Если 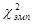 равно критическому значению или превышает его, расхождения между распределениями статистически достоверны. равно критическому значению или превышает его, расхождения между распределениями статистически достоверны.
|
Дата добавления: 2019-10-16; просмотров: 744;
