Обобщенный метод наименьших квадратов
Проблема эффективности линейной несмещенной оценки вектора b для обобщенной ЛММР решается с помощью теоремы Айткена.
Теорема Айткена: в классе линейных несмещенных оценок вектора b для обобщенной ЛММР оценка
| b* = (X’W-1X)-1X’W-1XY | (6.5) |
имеет наименьшую ковариационную матрицу (доказательство см. в работе [5, с.152]). При этом математическое ожидание оценки b* равно b: М(b*)=b, т.к. М(e)=0.
В случае классической модели, т.е. при выполнении требования åe=W=s2Еn , оценка b* обобщенного МНК совпадает с оценкой b обычного МНК.
Доказательство теоремы Айткена основано на утверждении матричной алгебры: если W - симметричная невырожденная матрица nxn, то она представима (хотя и неединственным способом) в виде произведения некоторых двух матриц:
| W=PP’, | (6.6) |
где Р - невырожденная матрица nxn.
От обобщенной модели Y=Xb+e путем умножения слева на обратную матрицу Р-1 перейдем к ее некоторому образу Y*:
| Y*= Р-1Y= Р-1Xb+ Р-1e=X*b+e*. | (6.7) |
Модель (6.7) удовлетворяет всем требованиям КЛММР. Следовательно, оценка b* по выражению (6.5) или аналогично (6.2):
| b*= (X*’X*)-1X*’Y* | (6.8) |
наиболее эффективна в классе всех линейных несмещенных оценок, являясь точкой минимума обобщенного критерия МНК:
| S*= åe*i2=e*’e*=(Y*-X*b)’(Y*-X*b)=e’We, | (6.9) |
где e*= Р-1e - см. выражение (6.7).
Для обобщенной регрессионной модели, в отличие от классической, коэффициент детерминации, вычисляемый в матричных обозначениях по формуле:
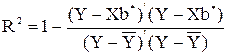
| (6.10) |
не является удовлетворительной мерой качества модели. Он может даже выходить за интервал [0; 1], и добавление (удаление) объясняющей переменной не обязательно приводит к его увеличению (уменьшению). Поэтому коэффициент детерминации используется только как приближенная характеристика.
Для практической реализации обобщенного МНК необходимо знать ковариационную матрицу W вектора возмущений, что случается весьма редко. Поэтому приходится вводить дополнительные условия относительно структуры матрицы W. Только тогда мы приходим к практически реализуемому обобщенному МНК. Наиболее важные виды структур матрицы W рассмотрим позднее.
Дата добавления: 2019-10-16; просмотров: 555;
