Устранение гетероскедастичности взвешенным МНК

Пусть проверка по тестам показала, что регрессионная модель (6.17) гетероскедастична:

Это означает, что дисперсии возмущений s_i² не равны между собой и сами возмущения e_i и e_k некоррелированы. Отсюда следует, что ковариационная матрица вектора возмущений å_e=W - диагональная:

.

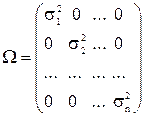(6.18)

Если дисперсии возмущений 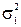известны, то гетероскедастичность легко устраняется. На практике, однако, эти значения никогда не бывают известны. Если исходить из предположения (6.15), то в качестве состоятельных оценок 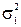берутся прогнозные значения 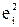регрессии (6.16).

Оценка параметров взвешенным МНК состоит в следующем.

1. Проверить с помощью одного или нескольких тестов факт наличия в исходной модели (6.17) гетероскедастичности.

2. Применить к модели (6.17) обычный МНК, найти оценочный вектор коэффициентов b, вычислить квадраты ошибок 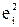- см. выражение (6.16).

3. Найти регрессию квадратов ошибок на квадратичные функции регрессоров, т.е. найти уравнение регрессии (6.16).

4. Вычислить по уравнению (6.16) прогнозные значения 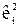и получить набор весов .

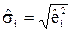5. Ввести новые переменные 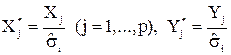и найти уравнение 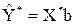, которое гомоскедастично. Полученная при этом оценка 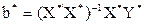- см. выражение (6.8) - и есть оценка взвешенного метода наименьших квадратов исходного уравнения (6.17).

Таким образом, неизвестные параметры уравнения регрессии находим:

- если применяем обычный метод наименьших квадратов, то минимизируя остаточную сумму квадратов:

S=e’e=å( 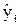-y_i)²;

- если применяем обобщенный метод наименьших квадратов, то минимизируя выражение:

S=e’W^-1e;

- если применяем взвешенный метод наименьших квадратов, то минимизируя взвешенную остаточную сумму квадратов:

S=å( 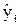-y_i)²/s_i.

В последнем случае мы добиваемся равномерного вклада остатков в общую сумму, что приводит к получению наиболее эффективных оценок параметров модели.