Устранение коррелированности регрессоров и ошибок методом инструментальных переменных
Суть метода состоит в подборе новых – инструментальных – переменных Zj (j=1, 2, … , h), которые тесно коррелируют с Xj и не коррелируют с e. Обычно количество инструментальных переменных Z не меньше, чем количество исходных переменных X. Соответствующая оценка параметров регрессии будет состоятельной:
| bZ=(Z’X)-1Z’Y=(Z’X/n)-1(Z’Y/n), | (7.1) |
где X, Y, Z – матрицы значений наблюденных переменных.
Для уравнения парной регрессии формула (7.1) примет вид:
 .
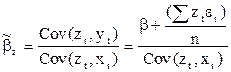| (7.2) |
Очевидно, что при n®¥ по вероятности bZ®b, что и означает состоятельность оценок (7.1) и (7.2), но отсюда не следует их несмещенность, не говоря уже об эффективности – минимальной ковариации.
Как находить нужные инструментальные переменные? В работе [6, с.181] отмечается: "Дать строгий однозначный ответ … невозможно. Все зависит от конкретной ситуации. Может так случиться, что инструментальных переменных нельзя найти, а может быть, что существует и несколько таких инструментов".
Например, если изучается зависимость Y – среднедушевых расходов семей на определенный товар (руб./чел.-мес.) от ненаблюдаемой переменной X – истинного среднедушевого дохода семей (руб./чел.-мес.), то в качестве инструментальной переменной можно взять Z – размер объявленного среднедушевого дохода семьи (руб./чел.-мес.).
Практическая реализация метода инструметальных переменных приводит нас к двухшаговому методу наименьших квадратов:
- сначала осуществляется регрессия Х на Z и находятся прогнозные значения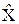 
, они теперь и будут считаться новыми независимыми переменными;
- искомая оценка вектора параметров b строится с помощью обычной регрессии Y на .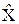
Таким образом, в двухшаговом МНК собственно МНК применяется дважды: сначала для построения регрессоров 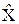, а затем для нахождении оценки b.
В заключение заметим, что вопрос о необходимости использования инструментальных переменных решается в форме проверки статистической гипотезы. Соответствующая процедура носит название теста Хаусмана.
Вопросы для самоконтроля
1. Каквовы свойства оценки "b" при коррелированности Xt и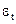 
?
2. Назовите две причины коррелированности регрессоров x и ошибок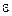 
.
3. Приведите пример инструментальных переменных.
4. В чем суть двухшагового метода наименьших квадратов?
Приложение 1
Основные понятия теории вероятностей
Дата добавления: 2019-10-16; просмотров: 439;